Flächenberechnung mithilfe der Integralrechnung

Question

Moin hab eine aufgabe und komm da irgendwie nicht weiter, ev hat wer eine Idee

Bestimmen Sie a∈ℝ+ so, das die Funktion f : ℝ\{0} → ℝ mit

f(x) = -(1/x)+10-x

im Intervall [a, a+1] die größtmögliche positive Fläche mit der x-Achse einschließt

Danke vom Voraus

Answer 1

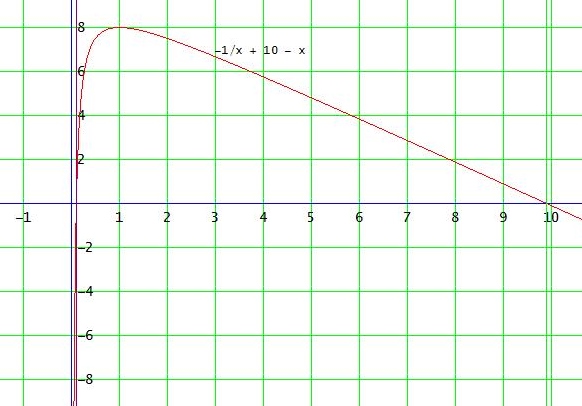
f(x) hat die Nullstellen  x₁ = 5 - 2·√6  und  x₂  = 2·√6 + 5  ( x₁ ≈ 0.101 ,  x₂ ≈ 9.899 )

Hier die Flächenberechnung für  x₁ ≤ a ≤ x₂ -1

( sonst musst du A_a =  | _a∫^x1 f(x) dx | + _x1∫^a+1 f(x) dx  bzw.  _a∫^x2 f(x) dx  + | _x2∫^a+1 f(x) dx | bzw. (für a≥x₂) |_a∫^a+1 f(x) dx | rechnen (#), weil dann ein Teil der Fläche unterhalb bzw. im letzten Fall die gesamte Fläche  unterhalb der x-Achse liegt. )

Eine Stammfunktion zu f(x) = -1/x + 10 - x  ist  F(x) = - ln(x) + 10x - 1/2·x² 

A_a =  _a∫^a+1 (-1/x + 10 - x) dx  = [ - ln(x) + 10x - 1/2·x² ]_a^a+1 

= -ln(a+1) + 10·(a+1) - 1/2 · (a+1)² - (- ln(a) + 10a - 1/2 · a²)

=  - ln(a + 1) + ln(a) - 1/2 ·(2·a - 19)  

Um das Maximum dieser Flächen zu bestimmen muss leitet man den letzten Term ab:

A_a' (a) =  - (a² + a - 1) / (a·(a + 1)) = 0

a₁ = - √5/2 - 1/2   ,  a₂ = √5/2 - 1/2

Bei a =  √5/2 - 1/2  wechselt A_a' (a)  das Vorzeichen von  + → - , dort wird die Fläche also maximal.

A_a(√5/2 - 1/2) = ln(3/2 - √5/2) - √5/2 + 10  

≈  7,919542361  FE   ist also die gesuchte maximale Fläche ( für x₁ ≤ a ≤ x₂ - 1 )

(#) für a < x₁ : 

 A_a(a) = | ln(a·(2·√6 + 5)) + a²/2 - 10·a - 10·√6 + 51/2 | 

                                 + (- ln((a + 1)·(2·√6 + 5)) - a²/2 + 9·a + 10·√6 - 16 ) 

Die Ableitung, die mein Rechner dazu angibt, ist abartig!

Gruß Wolfgang

Comments

Hallo Wolfgang,

ich möchte deine Ergebnisse bestätigen.

a = 0.618 und A = 7.92

Die andere Lösung mit a = -1.62 entfällt. Siehe deinen Graph.
Außerdem ist in der Aufgabenstellung a > 0 definiert.

mfg Georg