Aufgabe: Finde die Eigenwerte von 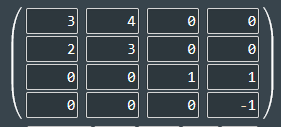
Text erkannt:
\( \left(\begin{array}{|r|r|r|r|}\hline 3 & 4 & 0 & 0 \\ \hline \hline 2 & 3 & 0 & 0 \\ \hline \hline 0 & 0 & 1 & 1 \\ \hline \hline 0 & 0 & 0 & \hline-1 \\ \hline\end{array}\right) \)
Problem/Ansatz:
Moin, ich wollt mal was anderes als immer dieselbe Methode mit dem charakt. Polynom probieren. Daher dachte ich, wenn ich eine Dreiecksmatrix erzeuge könnte ich die EWs einfach ablesen. Umgebaut nach Zeile 2 ergibt das  .
.
Leider stimmen die EWs der beiden Methoden nicht überein. Wo ist mein Denkfehler? Ich hatte gehofft, ich könnte die Dreiecksmatrix als Abkürzung verwenden.
Text erkannt:
\begin{tabular}{|r|r|r|r|}
\hline 3 & 4 & 0 & 0 \\
\hline \hline 0 & \( 1 / 3 \) & 0 & 0 \\
\hline \hline 0 & 0 & 1 & 1 \\
\hline \hline 0 & 0 & 0 & -1 \\
\hline
\end{tabular}