Aufgabe:
Gegeben ist die Funktionenschar \( \mathrm{t}_{\mathrm{k}} \) mit \( \mathrm{t}_{k}(\mathrm{x})=\mathrm{x} \cdot \mathrm{e}^{-0,5 k \cdot x^{2}} \)
Ohne Nachweis kann im Folgenden benutzt werden:
\( \mathrm{f}_{k}^{\prime}(\mathrm{x})=\left(1-\mathrm{k} \cdot \mathrm{x}^{2}\right) \cdot \mathrm{e}^{-0,5 k x^{2}} ; \mathrm{f}_{\mathrm{k}}^{\prime \prime}(\mathrm{x})=\mathrm{k} \cdot \mathrm{x} \cdot\left(\mathrm{k} \cdot \mathrm{x}^{2}-3\right) \cdot \mathrm{e}^{-0.5 \mathrm{k} x^{2}} \)
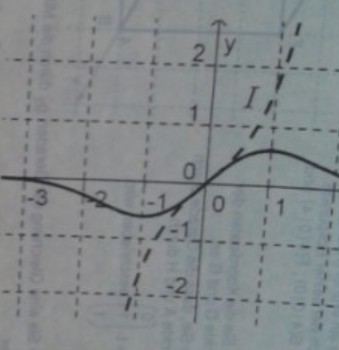
a) In der Abbildung sind die Graphen zu \( \mathrm{f}_{1} \) und \( \mathrm{f}_{-1} \) dargestellt.
Entscheiden Sie, welcher Graph zu \( f_{1} \) gehört.
Untersuchen Sie das Symmetrieverhalten der Ableitungsfunktion \( \mathrm{f}_{1}^{\prime} \).
Weisen Sie nach, dass die Gerade zu \( \mathrm{y}=\mathrm{x} \) Tangente an alle Graphen von \( t_{k} \) im Ursprung ist.
Untersuchen Sie, ob es möglich ist, den Parameter \( \mathrm{k} \) so zu wählen, dass der Graph von \( \mathrm{t}_{k} \) den Punkt \( \mathrm{H}(2 \mid 1) \) als Hochpunkt hat.
b) Bestimmen Sie in Abhängigkeit von k die Wendepunkte der Graphen von f_{k}.
c) Bestimmen Sie den \( y \)-Achsenabschnitt der Tangente an den Graphen von \( f_{1} \) im Punkt \( P\left(2 \mid f_{1}(2)\right) \).
Zeigen Sie, dass für den \( y \)-Achsenabschnitt \( \mathrm{b}(\mathrm{u}) \) einer Tangente an den Graphen von \( \mathrm{f}_{1} \) im beliebigen Punkt \( P_{u}\left(u \mid f_{1}(u)\right) \) gilt: \( b(u)=f_{1}(u)-f_{1}^{\prime}(u) \cdot u . \)
Ermitteln Sie den größten \( y \)-Achsenabschnitt, den eine Tangente an den Graphen von f, haben kann.
Untersuchen Sie, ob alle Punkte auf den Graphen von \( f_{k} \), in denen die Tangenten waagerecht verlaufen, auf einer Geraden durch den Ursprung liegen.
Ansatz/Problem:
Zu dem ersten Teil mit der Tangente:
Ich für f´(0) = 1 und nicht 0 also passt das mit der Aussage nicht.
zu dem Parameter:
Ich hab für k = 0,25 mit f´(2) = 0
das passt aber nicht, wenn man es in die Gleichung für f(x) einsetzt (nicht gleich 1 bei 2).