Zeichne dir die Punkte doch einfach mal in ein Koordinatensystem!
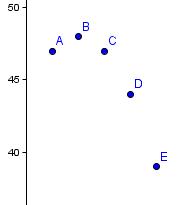
Das sieht doch stark nach einer Parabel aus.
Guckt man sich die Abweichungen vom Scheitelwert 48 an, so sieht man außerdem:
48-47 = 1
48-44 = 4
48-39 = 9
also die ersten drei Quadratzahlen!
Die Parameterdarstellung einer quadratischen Funktion ist
f(x) = a*(x-b)2+c
Wobei a die Streckung/Stauchung der Parabel ist (liegt hier nicht vor, da die oben ausgerechneten Differenzen genau die ersten Quadratzahlen sind, die Parabel ist aber nach unten geöffnet also a=-1.)
Der Scheitelpunkt (=die Spitze der Parabel) liegt dann bei (b, c).
Guckt man sich die Zeichnung nochmal an, so sieht man, dass der Scheitelpunkt bei (2, 48) liegt. Die Funktionsgleichung lautet also:
f(x) = -(x-2)2+48 = 48 - (x-2)2
Vorausgesetzt natürlich, du wählst die einfachst mögliche Lösung. Es gibt natürlich unendlich viele Kurven, die durch diese 5 Punkte gehen, aber diese ist die leichteste.
