ich sitze hier jetzt schon was länger an einer Matheaufgabe, jedoch komme ich nicht auf das gewünschte Ergebnis. Ich soll zeigen, ob folgende Mengen gleich sind:
(A \ B) ∪ (B \ A) = (A ∪ B) \ ( A ∩ B)
Ich habe mir das anhand eines Beispiels verdeutlicht. Daraus hat sich für mich ergeben dass die Mengen gleich sind.
Das ist mein aktueller Lösungsansatz, jedoch komme ich nicht auf die rechte Seite, der Fehler sollte eigentlich nicht allzu groß sein, oder ich übersehe eine einfache Umformung. Ich habe damit schon ein bisschen gespielt und mithilfe der De Morganschen Gesetze versucht die Zeichen umzudrehen aber das hat mich bisher auch nicht weiter gebracht.
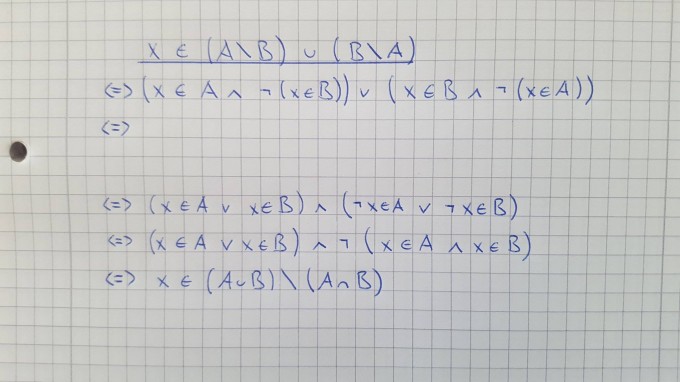
Vielleicht kann mir jemand von euch einen Tipp geben was ich jetzt wie umformen muss dass ich auf die geforderte Lösung komme.