das Video ist echt mega!
Habe mir das ausm Video notiert und habe es verstanden:
>Auf wie viele Arten kann man 7 Hotelgäste in 10 freien Einzelzimmern unterbringen?
Welche Formel?
Schritt 1:
Wie viele Wahlmöglichkeiten gibt es im ersten Schritt; wie viele im zweiten etc.?
Wenn sich die Zahl der Optionen pro Schritt ändert:
Ohne Zurücklegen
also kommen die Formeln A=(n über k)*k! und A=(n über k) infrage.
Wenn sich die Zahl der Optionen nicht pro Schritt ändert, dann:
Mit Zurücklegen
also kommen die Formeln n^k und A=(k+n-1 über k) infrage.
Schritt 2:
Hat man nach einer Reihenfolge eine wirkliche Veränderund, oder ist es eigentlich dasselbe?
Im Video schön dargestellt:
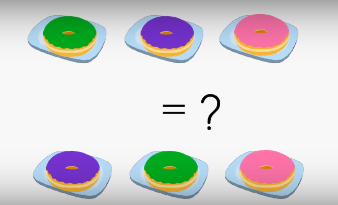
Die Frage zu beantworten kommt ganz auf den Zusammenhang an und muss in der Frage sein. Es kann sein, dass es relevant ist die Donuts so zu sortieren, weil z.B jemand sonst austickt oder durch irgendwelche anderen banalen Gründe.
Macht es etwas aus? ---> geordnet (Reihenfolge spielt eine Rolle)
Macht es nichts aus? → ungeordnet (Reihenfolge spielt keine Rolle)
Um Auf die Frage zurückzukommen:
Es werden pro Schritt immer weniger Wahlmöglichkeiten (Wenn ein Individuum einem Zimmer zugeteilt wird, sind es immer eine Option weniger). Also schonmal "ohne Zurücklegen"
Ist es vielleicht eigentlich dasselbe?
Nein! Es macht etwas aus, wer auf welches Zimmer verteilt wird.
Das heißt ---> geordnet.
Conclusion:
Wir müssen also geordnet, ohne Zurücklegen verwenden:$$ A=\begin{pmatrix} n \\ k \end{pmatrix} \cdot k! $$ Wir können n=10, k verschiedene Möglichkeiten zuteilen, also: $$A=\begin{pmatrix} 10 \\ 7 \end{pmatrix} \cdot 7! = 604800$$