Falls du gerade Kombinatorik durchnimmst, ist das vielleicht hilfreich für dich.
Die richtige Formel zu finden, damit habe ich auch Probleme gehabt. Vielleicht hilft dir das. Ich habe einen kleinen "How to find the right Formula Test". Beantworte die Frage und finde zur richtigen Formel:
Permutation? Ja oder Nein?
---> Bei einer Permutation werden alle Elemente der Grundmenge betrachtet. Wenn es keine Permutation ist wird nur eine Stichprobe der Grundmenge betrachtet.
Wenn Ja:
Permutation, ohne Wiederholung:
(Objekte, von denen alle unterscheidbar sind)
Formel: n! n= Grundmenge z.B (die Zahlen 1-10 (alle unterscheidbar))
Permutation, mit Wiederholung:
(Objekte, von denen manche nicht unterscheidbar sind):$$\frac{n!}{k_{1} \cdot k_{2} \cdot ... \cdot k_{s}}$$ Hierbei steht "k" für die verschiedenen Gruppen. Sagen wir "Auf wie viele Arten kann man 5 weiße und 3 rote Kugeln anordnen?"
Dann ist eine Gruppe (k1) die 5 weißen Kugeln und die andere Gruppe (k2) 3 Kugeln. Zusammen sind es 8 also "n".$$\frac{8!}{5! \cdot 3!}=56$$
2. Frage wenn Permutation Ja
Gibt es mehrere Grundmengen? Falls Ja:
Produktregel:$$n_{1}\cdot n_{2} \cdot ... \cdot {n_k}$$"Du hast 3 Socken, fünf Schuhe und 6 T-Shirts. Auf wie viele Arten kannst du diese Anziehen?$$3 \cdot 5 \cdot 6= 90$$Permutation? Nein!:
Die erste Frage, die du dir stellen solltest:
Wie viele Möglichkeiten gibt es im ersten und in den Folgezügen? Bleibt es immer gleich nach jeden Zug, wie hier?
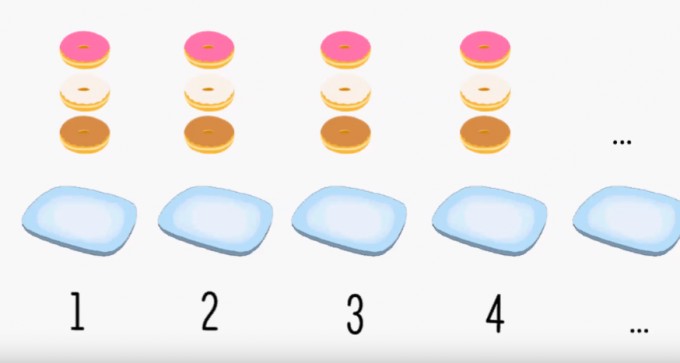
Wenn es so ist wie im Bild über diesem Text dann ist es schonmal: Mit Zurücklegen
Wenn es jeden Zug immer eine Option weniger wird, wie z.B hier:

Dann wissen wir schonmal es ist ---> Ohne Zurücklegen
Die nächste Frage die du dir stellen solltest lautet wie folgt:
Hat man nach einer Reihenfolgenänderung eine wirkliche Veränderung, oder ist es eigentlich dasselbe?
Wenn wir bei den Donuts bleiben z.B:
Ist es egal ob auf dem ersten Teller ein pinker Donut, ein weißer oder ein schwarzer Donut liegt?
Das kommt komplett auf den Kontext an und ist von jeder Aufgabe anders. Hier würde ich sagen, dass es egal ist. Bei manchen ist es auch deutlicher.
Macht es etwas aus? → geordnet
Macht es nichts aus? ----> ungeordnet
Formeln:
geordnet, ohne Zurücklegen:$$n^k$$geordnet, ohne Zurücklegen:$$\begin{pmatrix} n \\ k \end{pmatrix} \cdot k!$$ungeordnet, ohne Zurücklegen:$$\begin{pmatrix} n \\ k \end{pmatrix}$$ungeordnet, mit Zurücklegen:$$\begin{pmatrix} n+k-1 \\ k \end{pmatrix}$$Die anderen Formeln, falls Permutation Ja, siehst du ja weiter oben.
Beziehen wir das auf deine Frage:
Man hat 300 Sitzplätze und 150 Studierende. Wieviele Sitzplatzverteilungen sind möglich, wenn man annimmt, dass auf einem Sitzplatz maximal 1 Studierender sitzt.
Werden alle Elemente der Grundmenge betrachtet?
Nein, da nur 150 Plätze von 300 belegt werden. Die Grundmenge ist 300.
Haben wir nach jeden Zug weniger Optionen?
Ja, da wir immer einen Student weniger haben, wenn er sich setzt. Ohne Zrücklegen
Haben wir nach einer Reihenfolgenänderung eine wirkliche Veränderung?
Ja, denn es darf kein Student zwei mal am selben Ort sitzen, wenn die anderen auch gleich sitzen. --> geordnet$$ \begin{pmatrix} 300 \\ 150 \end{pmatrix} \cdot 150! \approx 5.36 \cdot 10^{351} $$
