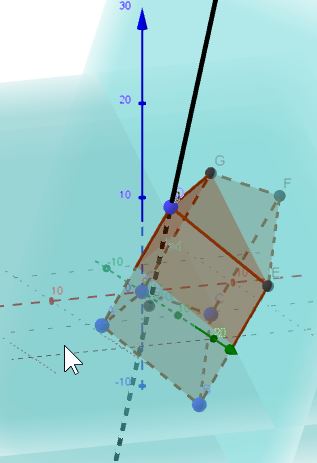
Das Viereck ist ein Drachenviereck. Lösungsskizze:
Wenn die Ebene schon durch O geht, dann nehm ich den Punkt auch für die Parameterform:
\( H_E(r, s) \, := \, r \; \left(6, 4, -2 \right) + s \; \left(0, 16, -8 \right) \)
Die Normalenform
\(H1: \, \left(A \otimes B \right) \; \left(x, y, z \right) = 0\)
ergibt dann
H1: y + 2 * z = 0
g aus D und Normalenvektor H1
\(g(t): \vec{x} = D + t \; \left(0, 1, 2 \right) \)
g ∈ H1
\(5 \; t_o + 30 = 0, t_o=-6\)
S = g(-6) = (0,2,-1)
AC⊥ OB
\( \left(C - A \right) \; \left(B - O \right) = 0 \)
\(V_{OABCDEFG}= \left( \left(A - O \right) \otimes \left(B - A \right) \right) \; \left(D - A \right) =1440\)
Teilen wir OABCEDFG entlang der Mittelebene OBG
G=(-6,4,13)
H_{OBG}:=(G⊗B)((x,y,z))/48=0
\(H_{obg}: \, -5 \; x - y - 2 \; z = 0\)
oder auf Höhe AD/2 parallel zu H_E
H_{ad}:=(0,1,2) ((x,y,z)-(A+(D-A)/2))=0
\(H_{ad}: \, y + 2 \; z - 15 = 0\)
Das Bild liefere ich dann dazu...