Aufgabe:
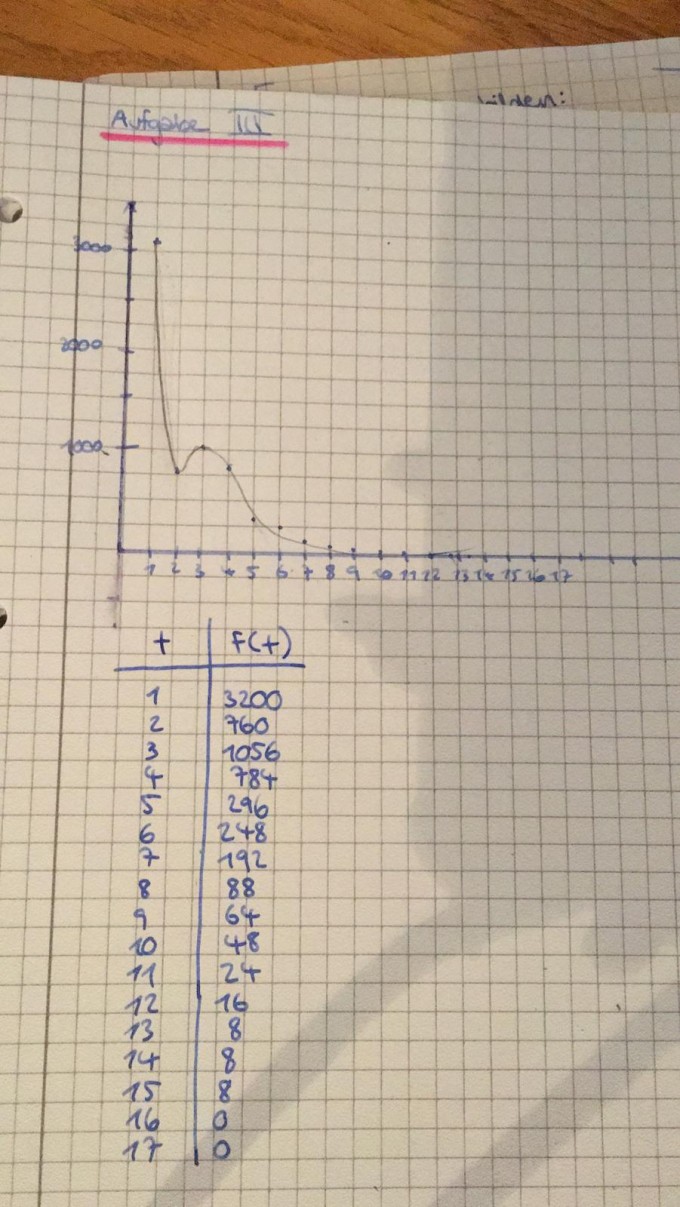
Folgende der Graph ist dargestellt. Der Graph wurde zu nächst in zwei Teile auf geteielt.
f(t) = {g(t) für t < 4; h(t) für t ≥ 4}
Dabei wurde g(t) bereits bestimmt, wenn man davon ausgeht das es sich um eine Funktions drittengrades handelt:
g(t) = -1652/3x³ +4672x² -37804/3 x +11680
Leider finde ich nicht die richtige bze. passende Funktionsart für h(t), dachte zuerst an Expoentialfunktion aber habe festgestellt das Werte die x - Achse schneiden somit verfiel die letzte Idee? Hat einer eine Idee und kann mir bei der bestimmung der Funktionsgleichung helfen bitteee.