Für ein Echtzeitsystem sind diese Angaben eher unrealistisch (Millisekunden wären weitaus glaubwürdiger!). Für den Echtzeitnachweis musst Du die erste und zweite Echtzeitbedingung prüfen. Du hast insgesamt drei Prozesse \(p_1\), \(p_2\) und \(p_3\).
1. Auslastung
Die Gesamtauslastung des Systems darf maximal \(100\%\) betragen.$$\sum\limits_{k=1}^{n}{\dfrac{C_k}{T_k}}\leq 1$$Dabei ist \(C_k\) die Verarbeitungszeit von Prozess \(k\) und \(T_k\) die Zykluszeit von Prozess \(k\). Da auf dem System \(3\) Prozesse laufen, ist \(n=3\) und wir berechnen:$$\sum\limits_{k=1}^{3}{\dfrac{C_k}{T_k}}=\dfrac{10}{30}+\dfrac{15}{45}+\dfrac{15}{60}=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{11}{12}<1\text{ }\surd$$
2. Pünktlichkeit
Ob die Prozesse einplanbar sind, musst Du nun graphisch lösen. Dabei ist \(C(t)\) die noch zu erbringende Rechenzeit. Du gehst dabei wie folgt vor:
- Bei \(t=0\) addierst Du die Verarbeitungszeiten aller Prozesse.
- Du zeichnest eine Strecke mit der Steigung \(-1\) vom Schnittpunkt mit der \(y\)-Achse bis zu dem Zeitpunkt, an dem ein anderer Prozess die Verarbeitung starten möchte (ergibt sich aus der Zykluszeit). Dies ist erstmalig bei \(t_1=30\) (Prozess \(1\)) der Fall. Es können zu einem bestimmten Zeitpunkt auch mehrere Prozesse starten wollen.
- An diesem Punkt addierst Du die Verarbeitungszeit des Prozesses (bzw. der Prozesse) und erhältst eine Verschiebung in \(y-\)Richtung.
- Diese Schritte (Strecke zeichnen, Verarbeitungszeiten der Prozesse an den entsprechenden Punkten addieren, ...) führst Du nun so lange weiter, bis Du den ersten Schnittpunkt mit der \(y-\)Achse erhältst. Der Verlauf sieht dann in etwa so aus:
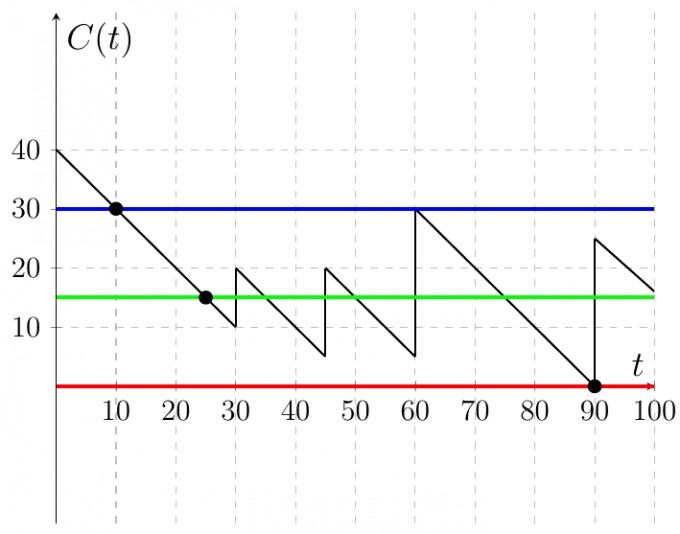
Der Schnittpunkt mit der \(y-\)Achse entspricht der tatsächlichen Reaktionszeit des niedrigstprioren Prozesses (= der mit der größten Zykluszeit). Nun zeichnest Du Parallelen zur \(x-\)Achse, die sich durch eine Verschiebung in positive \(y-\)Richtung um die Verarbeitungszeit des Prozesses ergibt, für den die Reaktionszeit bestimmt wurde. Der jeweils erste Schnittpunkt (von links aus gesehen) mit dem schwarzen Graphenverlauf ergibt die (tatsächlichen) Reaktionszeiten für den Prozess \(2\) (Schnitt mit der grünen Parallelen) und \(1\) (Schnitt mit der blauen Parallelen).
Nun musst Du nur noch die graphisch ermittelten tatsächlichen Reaktionszeiten mit den maximal zulässigen Reaktionszeiten vergleichen. Man sieht, dass die tatsächliche Reaktionszeit von Prozess \(3\) bei \(90s\) und somit über der maximal zulässigen Reaktionszeit (\(60s\)) liegt. Damit ist die zweite Echtzeitbedingung nicht erfüllt!