Hmm, ich war einfach davon ausgegangen, dass du schon weißt, was eine Ableitung ist, ansonsten ist es nämlich ziemlich schwer, die Funktion zu lösen - die Ableitung einer Funktion gibt ihre Steigung an einer bestimmten Stelle an.
Der Begriff der Steigung tritt z.B. bei linearen Funktionen (z.B. f(x) = 2x+1) auf. Hier ist die Steigung überall die gleiche und beträgt im Beispiel 2.
Bei komplizierteren Funktionen (in deiner Aufgabe kommt eine Parabel vor) ist die Steigung nicht überall die gleiche! Das siehst du direkt, wenn du die Funktion mal zeichnest.
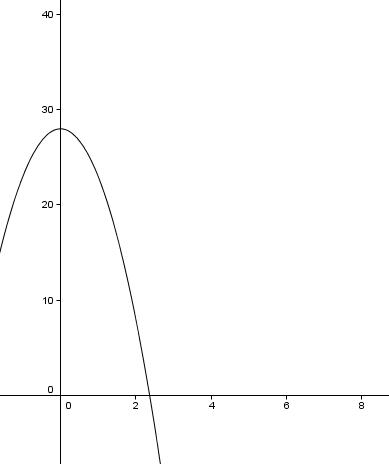
Wie du siehst, wird die Funktion immer steiler. Um die Steigung an einer Stelle herauszufinden, musst du die sogenannte momentane Änderungsrate oder auch Ableitung bestimmen.
Jetzt ist wieder die Frage, in welcher Klasse du bist und wie weit du schon im Stoff drin bist: um die Ableitung zu berechnen, muss man für gewöhnlich den sogenannten Grenzwert des Differenzenkoeffizienten berechnen.
Das heißt, du zeichnest quasi ein Steigungsdreieck in die Funktion ein (an der Stelle, die du untersuchst) und schiebst die beiden Punkte dann immer näher aneinander, so dass sich die Steigung des Dreiecks immer mehr der Steigung der Funktion annähert.
Man führt dabei einen sogenannten Grenzwert des Punktabstands gegen 0 durch. Man notiert das so:
$$ \lim _ { h \rightarrow 0 } \frac { f ( x + h ) - f ( x ) } { h } $$
Das ist die Formel der Steigung des Steigunsdreieck, dass sich vom Punkt (x, f(x)) aus zum Punkt (x+h, f(x+h)) aus erstreckt.
Das lim bedeutet Limes und steht für die Grenzwertdurchführung (also dass man h immer näher gegen 0 schiebt. Setzt man nun die ermittelte Nullstelle im Beispiel und die Funktion aus dem Beispiel ein, so erhält man:
$$ \lim _ { h \rightarrow 0 } \frac { f ( x + h ) - f ( x ) } { h } = \lim _ { h \rightarrow 0 } \frac { 28 - 5 ^ { * } ( 2,366 + h ) ^ { 2 } - \left( 28 - 5 ^ { * } ( 2,366 ) ^ { 2 } \right) } { h } \\ \lim _ { h \rightarrow 0 } \frac { - 5 * 2 * 2,366 ^ { * } h - 5 h ^ { 2 } } { h } = \lim _ { h \rightarrow 0 } \frac { 23,66 ^ { * } h - 5 h ^ { 2 } } { h } = \lim _ { h \rightarrow 0 } ( 23,66 - 5 h ) $$
Wenn man jetzt h immer kleiner macht (also den Grenzwert ausführt) dann ändert sich an der 23,66 nichts, nur das -5h verschwindet irgendwann. Das Ergebnis ist also 23,66.
Den zweiten Schritt habe ich relativ stark verkürzt, komplett ausgerechnet sieht der Zähler so aus:
28-5*(2,366+h)²-(28-5*2,366²) = 28-28 -5*(2,366²+2*2,366*h+h²) +5*2,366²
= -5*2,366²+5*2,366² +5*2*2,366*h + 5h² = 10*2,366*h+5h²