Aufgabe:
Bei \( 0^{\circ} \mathrm{C} \) wird in einem Skilager heißer Kaffee ausgeteilt, der in den Bechern abkühlt. In der Abbildung ist die exponentielle Abkühlungskurve des Kaffees dargestellt.
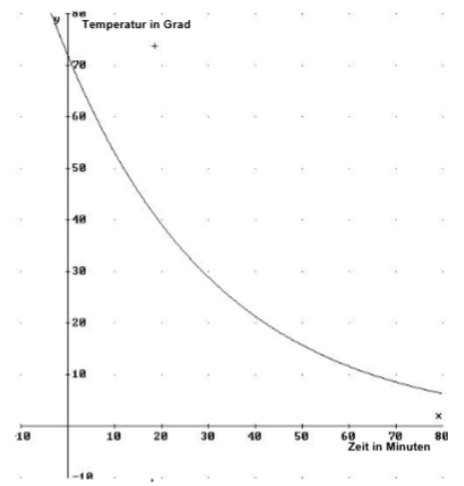
a) Bestimme aus der Zeichnung, welche Temperatur der Kaffee nach \( 20 \mathrm{~min} \) hat und wie lange man warten muss, wenn man den Kaffee mit \( 60^{\circ} \mathrm{C} \) trinken möchte.
b) Bestimme die zur Grafik gehörende Funktionsgleichung und überprufe rechnerisch die in a) abgelesenen Werte.
II. In der Skihütte herrscht vor dem warmen Kamin die Umgebungstemperatur von \( 21,4^{\circ} \mathrm{C} \). Auch dort wird Kaffee ausgeschenkt und Andi misst die folgenden Temperaturen:
| Zeit in min | 0 | 5 | 10 | 15 | 20 | 30 | 80 |
| Temperaturen in °C | 72 | 64,9 | 58,7 | 53,4 | 48,9 | 41,7 | ? |
a) Zeichne zur Wertetabelle den Grafen in das obige Koordinatensystem und beschreibe, was sich am Abkühlungsprozess im Vergleich zu I) ändert. Gib für \( 80 \mathrm{~min} \) einen Schätzwert für die Temperatur an.
b) Erläutere, dass die Funktionsgleichung für die Abkühlung des Kaffees hier die Form \( \mathrm{y}=\mathrm{a} \cdot \mathrm{b}^{\mathrm{x}}+\mathrm{c} \) hat und bestimme die zugehörigen Werte \( a, b \), und \( c \).