Der Graph einer ganzrationalen Funktion dritten Grades ist punktsymmetrisch zum Ursprung
f(x) = ax^3 + bx
f'(x) = 3ax^2 + b
und schneidet den Graphen von g(x) = 1/2(4x3 + x) = 2x^3 + 0.5x im Ursprung senkrecht.
f'(0) * g'(0) = -1
(3a*0^2 + b) * (6*0^2 + 0.5) = -1
b = -2
Ein zweiter Schnittpunkt mit g liegt bei x = 1 vor. Wie lautet die Funktionsgleichung?
f(1) = g(1)
a + b = 2.5
a = 2.5 - b = 2.5 - (-2) = 4.5
f(x) = 4.5x^3 - 2x
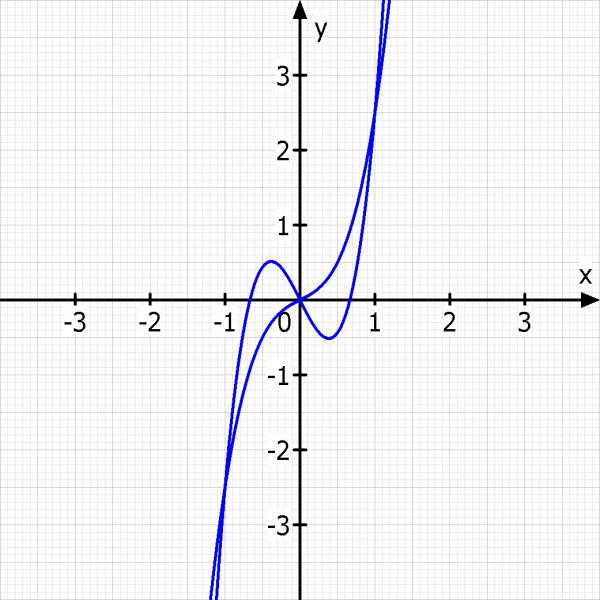
Skizze: