Hallo MP,
> f: ℝ \ {4} → ℝ
f(x)= 2 / (x-4)
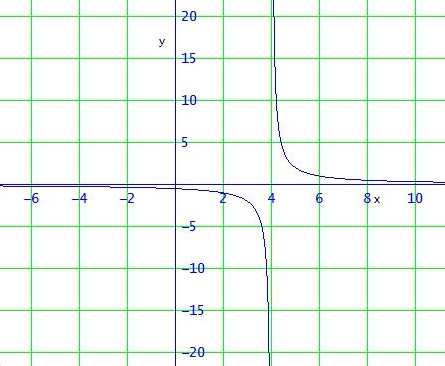
Der Graph der Funktion entsteht aus dem von y = 1/x durch Streckung in y-Richtung mit dem Faktor 2 und Verschiebung um 4 nach rechts (in x-Richtung).
Außer der x-Achse selbst (Gerade y=0) schneidet jede Parallele zur x-Achse den Graph von f genau einmal. Die Funktion ist also injektiv, weil jeder y-Wert nur höchstens einmal bei einem Punkt des Graphen vorkommt.
Sie ist aber nicht surjektiv, weil 0 ∈ ℝ kein Urbild in ℝ / {4} hat.
f: ℝ / {4} → ℝ \ {0} wäre dagegen bijektiv ( = injektiv und surjektiv. )
Gruß Wolfgang