Hallo Anton,
Nullstellen:
f(x) = -x4 + 32x2 - 6
Ersetze: z = x2
-z2 +32 z - 6 = 0 | * (-1 ) [ f(x) = ... | * (-1) macht keinen Sinn ]
z2 - 32z + 6 = 0
pq-Formel:
z1,2 = 32/2 ± √( (32/2)2- 6 )
= 16 ± √250 ≈ 16 ± 15,81
z1 ≈ 31,81 ; z2 ≈ 0,19
Ersetzung rückgängig machen:
x2 ≈ 31,81 oder x2 ≈ 0,19
x1,2 ≈ ± √31,81 ≈ ± 5,64 ; x3,4 ≈ ± √0,19 ≈ ± 0,44
Im Graph sind dass die Schnittstellen mit der x-Achse:
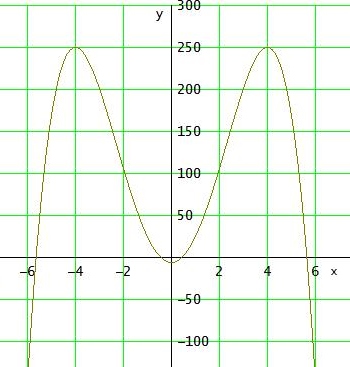
b)
Extremwerte:
Hier musst du doch mit den Nullstellen der Ableitung f ' arbeiten und nicht mit denen von f !
f '(x) = -4x3 + 64x = 0 ⇔ -4x * (x2 - 16) = 0
Extremstellen x1 = 0 ; x2,3 = ± 4
Mit deren Funktionswerten erhältst du dann den Tiefpunkt (0 | - 6)
und die beiden Hochpunkte (± 4 | 250)
Gruß Wolfgang