Mengen in Worten formulieren

Question

In Abb. 1 findet sich eine Prognose für die Anzahl der Studienanfängerinnen und -anfänger an österr. Hochschulen aus der Hochschulprognose 2014 der Statistik Austria. Sei (f) jene Funktion, die einem Jahr die Anzahl der Anfängerinnen und Anfänger zuweist. Bsp. ist f(2008) die Anzahl der Anfängerinnen/Anfänger für das Studienjahr 2007/08. Beantworten Sie dazu folgende Fragestellungen:

Formulieren Sie in Worten (ohne die Menge explizit zu bestimmen!)

\( \cdot\{j: f(j)<68000\} \)
\( \cdot\{f(j): 2010 \leq j \leq 2014\} \)
\( \bullet\{j:|f(j)-72000| \leq 1000\} \)

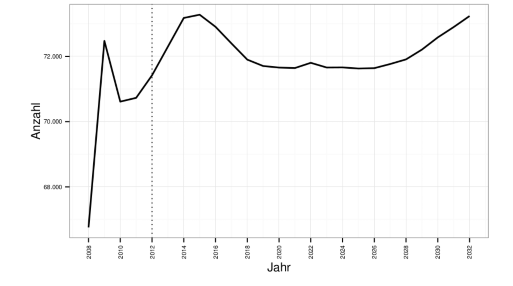
Kann mir da bitte jemand helfen? Herzlichen Dank.

Answer 1

{j:f(j)<68000} in Worten: Die Menge aller Jahreszahlen j von Jahren, in denen die Anzahl der Studienanfänger unter 68000 lag.

{f(j):2010≤j≤2014} in Worten: Die Menge aller Anzahlen von Studienanfängern in der Jahren von 2010 bis 2014 jeweils einschließlich.

Comments

Kannst du mir das auch noch mit dem Betrag erklären?

Text erkannt:

\( \cdot\{j:|f(j)-72000| \leq 1000\} \)

---

Beantworten Sie folgende Fragen symbolisch (d.h. wie oben), ohne Mengen zu bestimmen.

Wie viele Studienanfängerinnen gab es jeweils in den geraden Jahren?

---

{j:|f(j)−72000|≤1000} Die Menge aller Jahre, in denen die Anzahl von Studienanfängern um weniger als 1000 von 72000 abwich.

Die Menge der Anzahlen von Studienanfänger*innen in den geraden Jahren: {f(j):|mod(j,2)=0}