Hallo soll folgende Aufgabe lösen.
Aufgabe:
Erstellen Sie eine Skizze des Cam Carpets,
der für die dargestellte Figur, die eine quadratische
Gundfläche besitzt entsteht.
Die Seiten der Grundfläche sind 10 LE lang,
die Figur ist 6 LE hoch. Die Kameraposition sei \( (x, y, z)=(40,60,20) \)
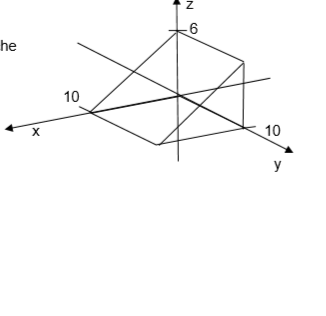
Mein Ansatz:
\( A=\left(\begin{array}{ccc}{1} & {0} & {\frac{-40}{20}} \\ {0} & {1} & {\frac{-60}{20}} \\ {0} & {0} & {0} \\\end{array}\right) \)
\( A=\left(\begin{array}{ccc}{1} & {0} & {-2} \\ {0} & {1} & {-3} \\ {0} & {0} & {0} \\\end{array}\right) \)
P1=\( \begin{pmatrix} 10\\0\\0 \end{pmatrix} \), P2=\( \begin{pmatrix} 10\\10\\0 \end{pmatrix} \)
P3=\( \begin{pmatrix} 0\\10\\0 \end{pmatrix} \),P4=\( \begin{pmatrix} 0\\10\\6 \end{pmatrix} \)
P5=\( \begin{pmatrix} 0\\0\\6 \end{pmatrix} \)
A*P
A*P1=\( \begin{pmatrix} 10\\0\\0 \end{pmatrix} \)
A*P2=\( \begin{pmatrix} 10\\10\\0 \end{pmatrix} \)
A*P3=\( \begin{pmatrix} 0\\10\\0 \end{pmatrix} \)
A*P4=\( \begin{pmatrix} -12\\-8\\0 \end{pmatrix} \)
A*P5=\( \begin{pmatrix} -12\\-18\\0 \end{pmatrix} \)
Ab hier weiß ich nicht weiter wäre dankbar, wenn mir einer einen Ansatz geben könnte.
Danke