Berechne wie hoch eine durch rotieren um die
x - Achse erzeugte Vase (Rotationskörper) sein muss, wenn der Boden der Vase einen Radins von
1,5 Längeneinheiten hat, der Anstiegswinkel 45" beträgt und das Volumen \( \frac{63 \pi}{8} \) Volumeneinheiten beträgt. Tipp: Das (gedachte) Koordinatensystem kann auch unterhalb der Vase beginnen.
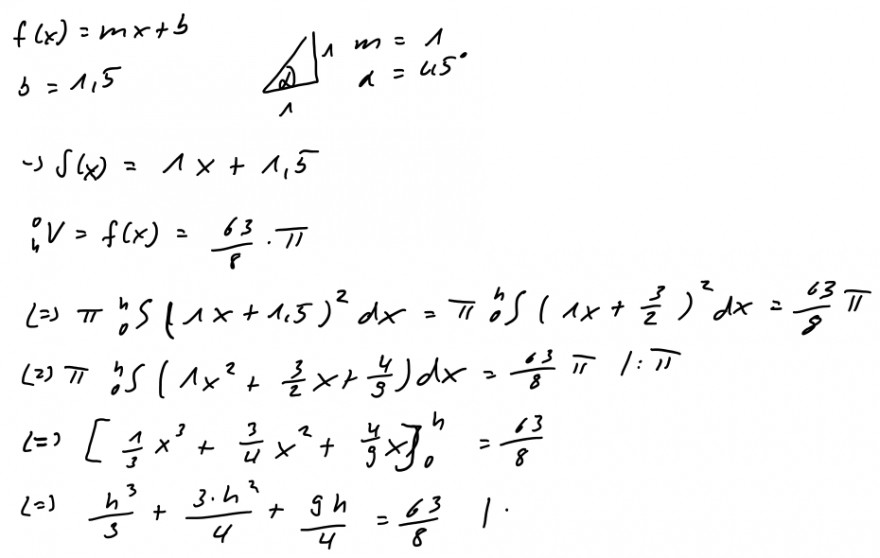
Text erkannt:
\( \begin{array}{ll}f(x)=m x+b & |\Delta| \begin{array}{c}m=1 \\ x\end{array}=u^{\prime} 5\end{array} \)
\( \Rightarrow S(x)=1 x+1,5 \)
\( i V=f(x)=\frac{63}{p} \cdot \pi \)
\( \Leftrightarrow \pi_{0}^{n} S(1 x+1,5)^{2} d x=\pi_{0}^{n} \int\left(1 x+\frac{3}{2}\right)^{2} d x=\frac{63}{8} \pi \)
\( (2) \pi \ln \left(1 x^{2}+\frac{3}{2} x+\frac{4}{9}\right) d x=\frac{13}{8} \pi / 1=\pi \)
\( \Leftrightarrow\left[\frac{1}{3} x^{3}+\frac{3}{4} x^{2}+\frac{4}{9} x\right]_{0}^{4}=\frac{13}{8} \)
\( \Leftrightarrow \frac{n^{3}}{3}+\frac{3 \cdot h^{2}}{4}+\frac{9 n}{4}=\frac{63}{8} \)
Text erkannt:
1. Berechne wie hoch eine durch rotieren um die
x - Achse erzeugte Vase (Rotationskörper) sein muss, wenn der Boden der Vase einen Radins von
1,5 Längeneinheiten hat, der Anstiegswinkel 45" beträgt und das Volumen \( \frac{63 \pi}{8} \) Volumeneinheiten beträgt. Tipp: Das (gedachte) Koordinatensystem kann auch unterhalb der Vase beginnen. 3 What is the
writers
is the
the the
Ich hab die Aufgabe angefangen aber ich weiß nicht ob das richtig ist was ich da gemacht habe. Ich komme auch nicht weiter bei der Aufgabe.
Kann mir da jemand helfen?