Berechnung des Winkels phi durch Vereinfachung der Formel: -2Rr = (sin phi)² / (cos phi)³ möglich?

Question

Zwei Kreise auf gleicher Achse mit dem Abstand R der Mittelpunkte zueinander, und dem Radius des kleineren Kreises r, schneiden sich genau an 2 Punkten (Spiegelung an der Mittelachse, bzw. wenn diese die X-Achse ist, an der X-Achse).

Diese ergeben sich aus den Winkeln mit der Formel:

  R · sin ε = r · sin φ
        sin ε = r/R · sin φ
sin ε/sin φ = r/R

  R · cos ε = ((R² – (r·sinφ)²))^0,5
  R · cos ε = R – r·cosφ
  R·(cos ε – 1) = -r · cos φ

  R – r·cosφ = ((R² – (r·sinφ)²))^0,5

R²-2Rr·cosφ+(r·cosφ)²=R²-(r·sinφ)²
-2Rr·cosφ + (r·cosφ)² = (r·sinφ)²

                     (r·sinφ)²

-2Rr·cosφ = ------------

                     (r·cosφ)²

             (sinφ)²        (1 - (cosφ)²)

-2Rr = -----------  = ------------------- = ?

             (cosφ)³          (cosφ)³

Answer 1

Es ist \(\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n\) und \(\frac{\sin\varphi}{\cos\varphi}=\tan\varphi\).

Comments

Guten Tag Oswald,

Danke für den Tip, den habe ich in die Formel eingebaut, aber es bleiben leider immer noch zwei Kreisfunktionen übrig, oder aber ich habe etwas nicht beachtet:

Text erkannt:

\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{(\mathrm{r} \cdot \sin \varphi)^{2}}{(\mathrm{r} \cdot \cos \varphi)^{2}} \)
\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{\sin \varphi^{2}}{\cos \varphi^{2}} \)
\( -2 \operatorname{Rr}=\frac{\sin \varphi^{2}}{\cos \varphi^{3}} \)
\( -2 \operatorname{Rr}=\tan \varphi^{2} \cdot \cos \varphi^{-1} \)
\( \arctan (\sqrt{(-2 \mathrm{Rr})})=\varphi \cdot \arctan (\sqrt{\left(\frac{1}{\cos \varphi}\right)}) \)

 Aber vielleicht geht es auch leichter. Vielen Dank.

Mit besten Grüßen ovj

Answer 2

Hallo,

wenn Du \(\varphi\) berechnen möchtest, so geht das wesentlich einfacher

Das Dreieck \(\triangle M_2BC\) ist ein rechtwinkliges (Tahleskreis). \(\varphi\) sei der blaue Winkel, \(r\) ist die grüne Strecke und der braune Durchmesser ist \(2R\). Du kannst direkt ablesen: $$\cos \varphi = \frac{r}{2R}$$

Comments

Guten Tag Werner-Salomon,

der Hinweis auf den Thaleskreis ist sehr gut. Danke. Was mir fehlt, ist das Verständnis für die Zusammenhänge zwischen dem Strahl, welcher durch C - M1 geht, und zu dem kleineren Kreis in Höhe  des Berührpunktes (Schnittpunkt des Strahls M2 -C mit dem kleineren Kreis) einen rechten Winkel bildet, zur Berechnung des Winkels zwischen den beiden Strahlen

1.) M2 - C

2.) M2 - M1 - B

Hintergrund: Der Strahl C - M1 könnte z.B. die Mittel-Linie eines Pleuels beinhalten, welches zwischen M1 - C montiert ist.

Der Punkt M1 könnte an der Quertraverse eines Rhomben-Antriebs, und der Punkt C am Mittelpunkt des Zapfens einer Kurbelwelle enden.

Die Strecke M2 - C könnte den Radius zwischen Mittelpunkt der KW und dem Antriebszapfen darstellen. Wenn sich eine einfache Lösung für eine Berechnungsmethode bilden ließe, wäre mit Hilfe der Tabellen-Kalkulation eine x-y-Chart ermittelbar, bei welcher die Achse M2 - M1 ebenfalls noch gedreht werden könnte, und die Tabellenkalkulation schnell Ergebnisse für einen Parallel-Offset liefern könnte. Denn eine Näherungsformel wie z.B.=

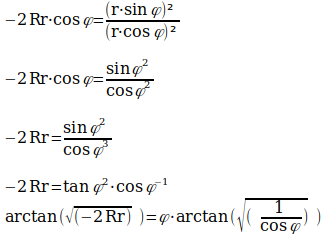
Text erkannt:

\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{(\mathrm{r} \cdot \sin \varphi)^{2}}{(\mathrm{r} \cdot \cos \varphi)^{2}} \)
\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{\sin \varphi^{2}}{\cos \varphi^{2}} \)
\( -2 \operatorname{Rr}=\frac{\sin \varphi^{2}}{\cos \varphi^{3}} \)
\( -2 \operatorname{Rr}=\tan \varphi^{2} \cdot \cos \varphi^{-1} \)
\( \arctan (\sqrt{(-2 \mathrm{Rr})})=\varphi \cdot \arctan (\sqrt{\left(\frac{1}{\cos \varphi}\right)}) \)

 

Text erkannt:

\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{(r \cdot \sin \varphi)^{2}}{(r \cdot \cos \varphi)^{2}} \)
\( -2 \operatorname{Rr} \cdot \cos \varphi=\frac{\sin \varphi^{2}}{\cos \varphi^{2}} \)
\( -2 \operatorname{Rr}=\frac{\sin \varphi^{2}}{\cos \varphi^{3}} \)

benötigt doch etwas Rechen-Zeit und dies ist ja nur eine Teil-Funktion im Gesamtumfang.

Zumal ein weiterer gegenläufiger Rhombenantrieb phasenversetzt laufen soll, um den geplanten Kompressionsprozeß energetisch optimieren zu können. Ideal wäre eine Niedertemperatur-Stelzer-Otto-Stirling-Kombination, mit Ein-Zylinder-Dreifach-Kolben-Kompressionsbereich ohne Ventile und aus Hochpräzisions-Leichtmetall-Keramik, Wasser geschmiert.

Aber manchmal sieht man vor lauter Bäumen den Wald nicht mehr.

Und ich suche einfach nur eine einfache Lösung, so wie z.B. die des Thaleskreises, wenn es die für vorgenannte Aufgabenstellung gibt. Danke für Ihre Zeit und Ihr Interesse. Mit besten Grüßen ovj