Aufgabe:
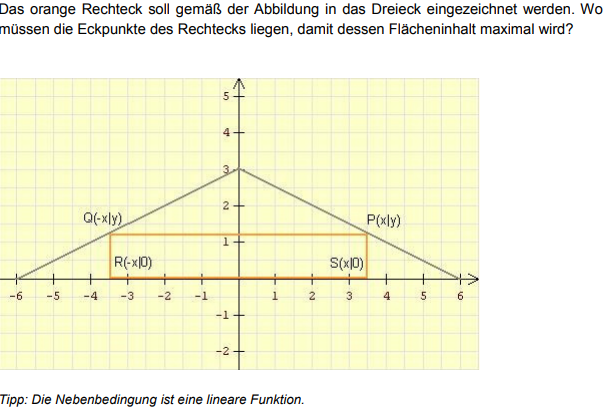
Das orange Rechteck soll gemäß der Abbildung in das Dreieck eingezeichnet werden. Wo
müssen die Eckpunkte des Rechtecks liegen, damit dessen Flächeninhalt maximal wird?
Text erkannt:
Das orange Rechteck soll gemaß der Abbildung in das Dreieck eingezeichnet werden. Wo
mússen die Eckpunkte des Rechtecks liegen, damit dessen Flächeninhalt maximal wird?
Tipp: Die Nebenbedingung ist eine lineare Funktion.
Problem/Ansatz:
Wie kann ich das berechnen?