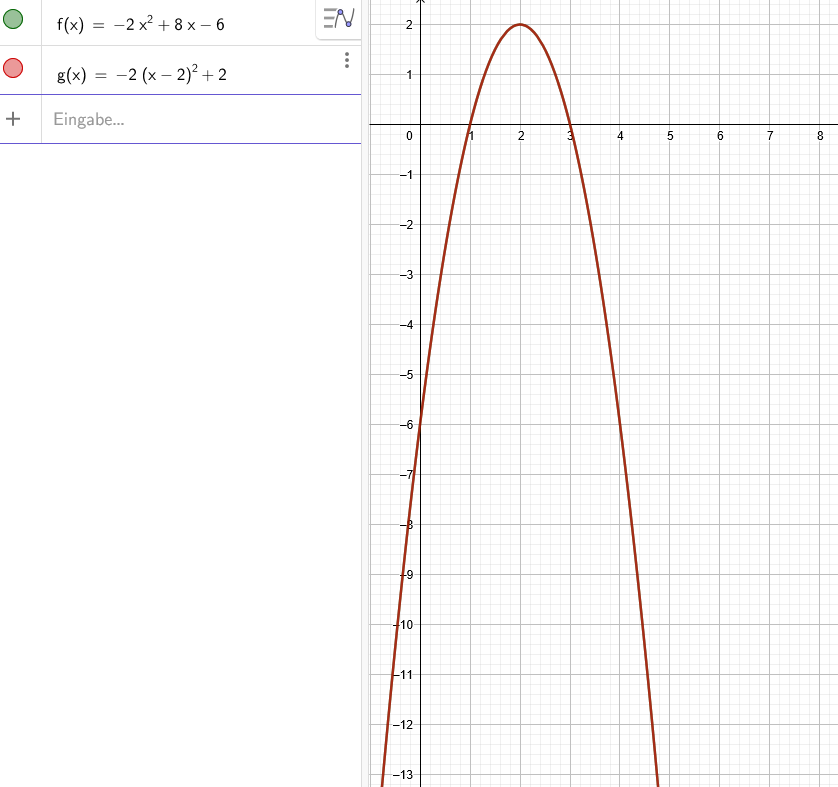
f(x) = −2x^2+8x−6
Du hast den Weg über die Scheitelpunktform gewählt: f(x)=-2*(x-2)^2+2 Das ist richtig. Du willst nun die Nullstellen finden:
-2*(x-2)^2+2=0|:(-2)
(x-2)^2-1=0|+1
(x-2)^2=1|\( \sqrt{} \)
\( \sqrt{(x-2)^2} \)=\( \sqrt{1} \)
|x-2|=1
1.) Fall (x-2)≥0
x-2=1
x₁=3
2.) Fall (x-2)<0
-(x-2)=1
-x+2=1
-x=-1
x₂=1
Ich zeige dir den direkten Weg zu den Nullstellen:
−2x^2+8x−6=0
2x^2-8x+6=0|:2
x^2-4x=-3
(x-2)^2=-3+4=1 Im Hinterkopf die oben aufgeführte Fallunterscheidung:
x₁=2+\( \sqrt{1} \)=3
x₂=2-\( \sqrt{1} \)=1
Text erkannt:
N