Ohne Substitution:
\( e^{2x} \) + 2\( e^{x} \) = 8
(\( e^{x} \) +1)^2 = 8+1 = 9|\( \sqrt{} \)
1.) \( e^{x} \) =-1+3=2 x=ln(2)
2.)\( e^{x} \) =-1-3= - 4 → keine Lösung in ℝ
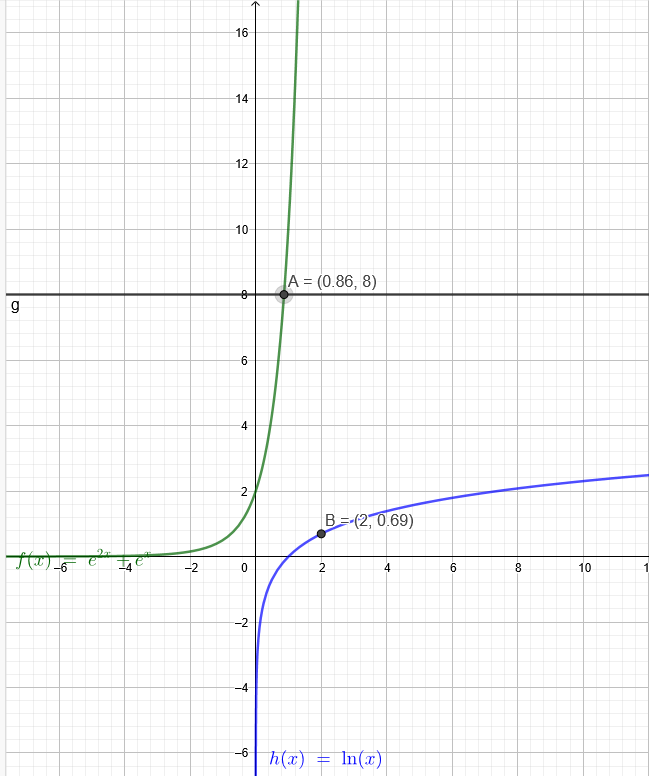
Ich stelle mal die Zeichnung GeoGebra ein. Da kommen verschiedene Werte raus. Wer kapiert das?
ln(2)≈0,69 Das müsste aber auch bei dem grünen Graph so sein!