In die Spalten deiner Abbildungsmatrix gehören die Bildvektoren der Basisvektoren (1,0) und (0,1).
Du kannst/sollst dir also im Koordinatensystem überlegen, welche Koordinaten die Bildvektoren dieser beiden Vektoren haben und bist dann fertig.
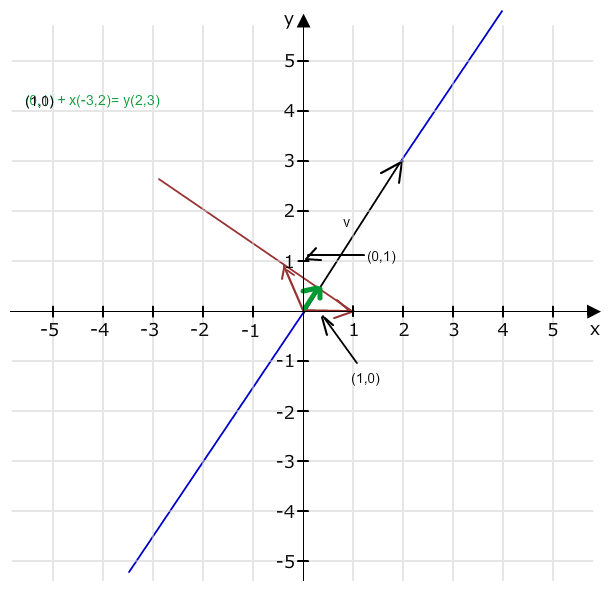
Spiegelungspunkt für (1,0) kannst du mit dem hellgrünen linearen Gleichungssystem in der Abbildung berechnen.
(1,0)+ x(-3,2) = y(2,3)
1-3x = 2y
2x = 3y
----> 3/13 = x
Danach bekommst du deinen ersten Spaltenvektor als a = (1,0) + 2x*(-3,2)
a= (1,0) +6/13 (-3,2) = (1-18/13 , 12/13) = (-5/13, 12/13)
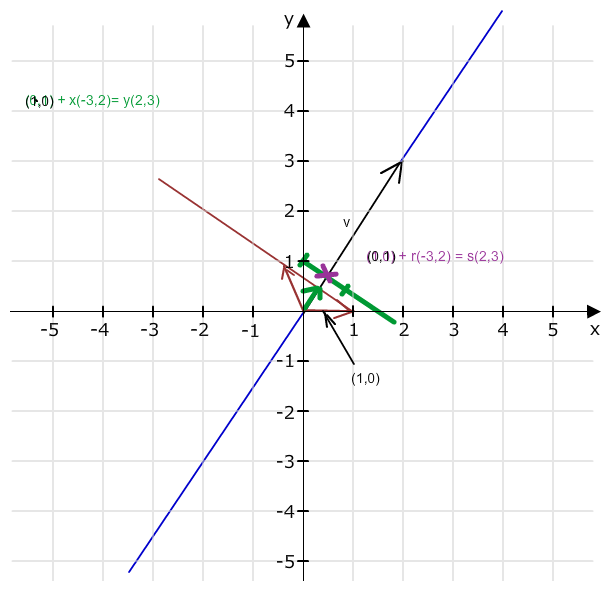
Wenn du das geschafft hast, spiegelst du noch (0,1) an der gegebenen Geraden. Skizze und Rechnung analog.
(0,1)+ r(-3,2) = s(2,3)
-3r = 2s
1 + 2r = 3r
-------> r= -2/13
Der zweite Spaltenvektor ist b = (0,1) + 2r(-3,2)
=(0,1) -4/13(-3,2)
= (12/13, 1-8/13) = (12/13, 5/13)
Die Spiegelungsmatrix wäre nun
A=
( -5/13 12/13
12/13 5/13)
Kontrolle: Determinante einer Spiegelungmatrix (Achsenspiegelung) sollte -1 sein
-25/169 - 144/169 = -169/169 = -1.
Daher sollte das nun stimmen.