Schnittpunkt zweier geraden berechnen, mittels vektoren

Question

Hallo,hier muss man den Schnittpunkt zweier geraden berechnen.Jedoch ist der Schnittpunkt S(2;2)Egal wie oft ich es rechne, bei mir kommt was anderes raus.Kann jemand über meine rechnung schauen, und mir sagen, was ich falsch mache.Ich danke im voraus.

Answer 1

g1: X = [3, 0] + r * [-2, 4]
g2: X = [-1, -3] + s * [3, 5]

Gleichsetzen

[3, 0] + r * [-2, 4] = [-1, -3] + s * [3, 5]

- 2·r - 3·s = -4
4·r - 5·s = -3    | II + 2*I

- 11·s = -11 → s = 1

4·r - 5·(1) = -3 → r = 1/2

Schnittpunkt

S = [3, 0] + 1/2 * [-2, 4] = [-1, -3] + 1 * [3, 5] = [2, 2]

Comments

3 + 2·(3/4 + 5/4·s) = -1 - 3·s

Wenn du das auflöst hast du erhalten

11/2 = -11/2·s → s = -1

Das sieht also auch gut aus. Du hast als Richtungsvektor nur die Gegenvektoren der üblichen Richtungsvektoren genommen. Das ist zwar nicht falsch. Macht man in der Regel aber nicht.

---

Danke für die ausführliche erklärung.

Ich habe gestern im Tutorium noch mal gefragt, ob es egal ist, wie man was von was abzieht, um den richtungsvektor zu bestimmen, und mein tut hat gesagt, dass es egal wäre.

Meine frage:

Welchen punkt zieht man am besten von was am besten ab, um den richtungsvektor zu bestimmen?

---

Ich habe ja geschrieben das es egal ist.

Das ist zwar nicht falsch. Macht man in der Regel aber nicht.

Die Gerade durch die Punkte A und B stellst du üblicherweise mit dem Richtungsvektor AB = B - A in folgender Form auf

X = A + r * AB

Du ziehst also vom Punkt B den Punkt A ab wenn du A als Stützvektor nimmst.

Wichtig ist sowas für andere Aufgaben, wenn du z.B. prüfen sollst, ob z.B. ein Punkt auf der Strecke AB liegt.

---

Super. Vielen Dank für die erklärung

Answer 2

Hallo,

du hast es doch schon fast richtig.

\( \begin{aligned} 3+2\left(\frac{3}{4}+\frac{5}{4} s\right) &=-1-3 s \\ 3+\frac{3}{2}+\frac{5}{2} s &=-1+s\\ 4+\frac{3}{2} &=-\frac{11}{2} s\\ \frac{11}{2} &=    -\frac{11}{2} s \\ s&=-1 \\ t&= -\frac12\end{aligned} \)

Nun noch einsetzen und ausrechnen.

:-)

Answer 3

Hallo Wolfi,

Kann jemand über meine rechnung schauen, und mir sagen, was ich falsch mache.

Dein "Fehler" war lediglich, dass Du kurz vorm Ziel aufgehört hast. Vervollständigt sähe Deine Rechnung so aus$$\begin{aligned} 4 + \frac 32 &= - \frac{11}2 s \\ \frac{11}2&= -\frac{11}2 s &&|\,\div \left(-\frac{11}2 \right) \\ -1 &= s\end{aligned}$$Einsetzen von \(s=-1\) in die Gleichung für \(g_2\) gibt$$\begin{aligned}g_2: \quad \vec x &=\begin{pmatrix}-1\\ -3\end{pmatrix} + s\begin{pmatrix}-3\\ -5\end{pmatrix} \\ \vec x(s=-1) &=\begin{pmatrix}-1\\ -3\end{pmatrix} +(-1)\begin{pmatrix}-3\\ -5\end{pmatrix}\\ &=\begin{pmatrix}-1\\ -3\end{pmatrix} +\begin{pmatrix}3\\ 5\end{pmatrix} \\&= \begin{pmatrix}2\\ 2\end{pmatrix}\end{aligned}$$das ganze nochmal im Plot

~plot~ -2(x-3);5(x+1)/3-3;{2|2};{3|0};{-1|-3} ~plot~

Comments

Uhhh, danke. Ich habe nicht verstanden, wo ich es am ende einsetzen soll.

---

Nch ein Tipp: es lohnt sich immer, sich das aufzuzeichnen. Und dort auch die berechneten Vektoren einzutragen. So kannst Du Dein Ergebnis direkt kontrollieren. Bzw. das Ergebnis auch vorweg nehmen.

Wenn Du von \(P_2\) aus, in Gegenrichtung - weil \(s \lt 0\) - um eine Pfeillänge auf der Geraden zurück läufst, kommst Du direkt bei \((2|\,2)\) heraus.

---

Ich habe nicht verstanden, wo ich es am ende einsetzen soll.

Ok - nochmal nachgefragt: ist Dir klar, was so eine Geradengleichung ...$$g_2: \quad \vec x=\begin{pmatrix}-1\\ -3\end{pmatrix}+ s\begin{pmatrix}-3\\ -5\end{pmatrix}$$...überhaupt aussagt? Also geometrisch betrachtet?

---

leider nicht ganz.

---

Schau Dir dieses Bild mit der Geraden \(g_2\) nochmal an

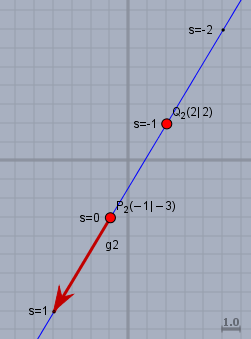
Die Gerade verläuft durch die Punkte \(P_2(-1|\,-3)\) und \(Q_2(2|\,2)\). Du hast dann einen Differenzvektor (rot im Bild) berechnet, indem Du beide Punkte von einander abgezogen hast. Und einen der Punkte (hier \(P_2\)) hast Du als Stützvektor gewählt.

Es ist dabei im Prinzip egal, wie Du die Differenz bildest und welchen Punkt Du als Stützvektor wählst. Nur einmal festgelegt, musst Du dabei bleiben. Und hier kommst Du eben zu$$g_2: \quad \vec x_2(s)=\begin{pmatrix}-1\\ -3\end{pmatrix}+ s\begin{pmatrix}-3\\ -5\end{pmatrix}$$mit diesem Ausdruck wird eine Menge von unendlich vielen Punkten beschrieben. Diese Punkte liegen alle auf einer Geraden - nämlich auf \(g_2\). Mit der Wahl des Wertes für den Parameter \(s\) kann man nun jeden beliebigen Punkt auf der Geraden \(g_2\) 'anfahren'.

Mit der Wahl von \(s=0\) kommt man immer zum Stützpunkt der Geraden und mit der Wahl von \(s=1\) kommt man immer an die 'Pfeilspitze' des Richtungsvektors, wenn man diesen am Stützpunkt anlegt.

Tue Dir mal selber einen Gefallen, nehme ein großes Blatt Papier (mit Kästchen) und berechne alle Punkte \(\vec x\) für \(s=-3\), \(s=-2\) usw. bis \(s=2\). Und zeichne die Punkte auf dem Paier ein. Wähle als Einheit ein Kästchen (nicht 1cm).

Der Trick bei der Schnittpunktberechnung ist nun, zwei Geraden gleich zu setzen$$\vec x_1(r) = \vec x_2(s)$$und nur dann, wenn ein Punktepaar \((r,\,s)\) diese Gleichung erfüllt, gibt es auch einen Schnittpunkt. Und es reicht dann aus, einen der Werte \(r\) oder \(s\) zu kennen und ihn in seine(!) Geradengleichung einzusetzen um den Schnittpunkt dann konkret zu berechnen.

Frag' ruhig nach, wenn noch was unklar ist.

---

Wow, danke für deine bemühungen