Bestimmen Sie eine Basis von Ker A = Ker μA .

Question

Aufgabe:

Es seien

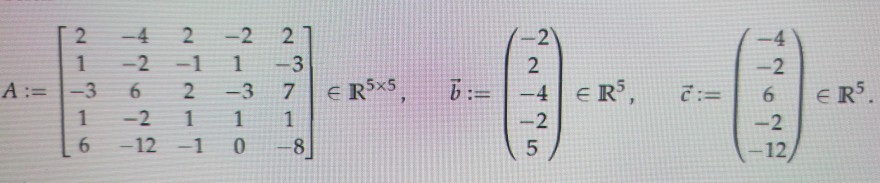
Text erkannt:

$A:=\left[\begin{array}{ccccc}2 & -4 & 2 & -2 & 2 \\ 1 & -2 & -1 & 1 & -3 \\ -3 & 6 & 2 & -3 & 7 \\ 1 & -2 & 1 & 1 & 1 \\ 6 & -12 & -1 & 0 & -8\end{array}\right] \in \mathbb{R}^{5 \times 5}, \quad \vec{b}:=\left(\begin{array}{c}-2 \\ 2 \\ -4 \\ -2 \\ 5\end{array}\right) \in \mathbb{R}^{5}, \quad \vec{c}:=\left(\begin{array}{c}-4 \\ -2 \\ 6 \\ -2 \\ -12\end{array}\right) \in \mathbb{R}^{5}$

a) Bestimmen Sie eine Basis von Ker A = Ker μ_A .

Problem/Ansatz:

Normalerweise soll oben links anstaat 2 eine 1 seien aber ich weiß es nicht , wie ich 2 weg kriegen kann? :(

Es wäre sehr nice, wenn jemand es vorrechnet.

Answer 1

Aloha :)

Wir lösen das Gleichungssystem mit elementaren Zeilenumformungen nach Gauß. Unser Ziel bei dem Vorgehen ist es, so viele Spalten wie möglich zu erhalten, die lauter Nullen und genau eine Eins enthalten.

$$\begin{array}{rrrrr|c|l}x_1 & x_2 & x_3 & x_4 & x_5 & = &\text{Aktion}\\\hline2 & -4 & 2 & -2 & 2 & 0 & -2Z_4\\1 & -2 & -1 & 1 & -3 & 0 &-Z_4\\-3 & 6 & 2 & -3 & 7 & 0 &+3Z_4\\1 & -2 & 1 & 1 & 1 & 0 &\\6 & -12 & -1 & 0 & -8 & 0 &-6Z_4\\\hline0 & 0 & 0 & -4 & 0 & 0 & \colon(-4)\\0 & 0 & -2 & 0 & -4 & 0 &\colon(-2) \\0 & 0 & 5 & 0 & 10 & 0 &\colon5\\1 & -2 & 1 & 1 & 1 & 0 &\\0 & 0 & -7 & -6 & -14 & 0 &\\\hline0 & 0 & 0 & 1 & 0 & 0 & \\0 & 0 & 1 & 0 & 2 & 0 & \\0 & 0 & 1 & 0 & 2 & 0 &-Z_2 \\1 & -2 & 1 & 1 & 1 & 0 &-Z_2-Z_1\\0 & 0 & -7 & -6 & -14 & 0 &+7Z_2+6Z_1\\\hline0 & 0 & 0 & 1 & 0 & 0 & \implies x_4=0\\0 & 0 & 1 & 0 & 2 & 0 & \implies x_3+2x_5=0\\0 & 0 & 0 & 0 & 0 & 0 & \\1 & -2 & 0 & 0 & -1 & 0 &\implies x_1-2x_2-x_5=0\\0 & 0 & 0 & 0 & 0 & 0 &\\\hline\end{array}$$Wir haben 2 Nullzeilen erhalten, die keine Bedingung an die Koordinaten stellen. Die anderen 3 Zeilen stellen jeweils eine Bedinung an die Koordinaten, die ich rechts in die Aktions-Spalte geschrieben habe. Wir können diese Bedingungen nach denjenigen $x_i$ umstellen, die genau eine 1 in der Spalte haben, also nach $x_1$, $x_3$ und $x_4$:$$x_4=0\quad;\quad x_3=-2x_5\quad;\quad x_1=2x_2+x_5$$Damit haben wir alle Vektoren des Kerns gefunden:$$\begin{pmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{pmatrix}=\begin{pmatrix}2x_2+x_5\\x_2\\-2x_5\\0\\x_5\end{pmatrix}=x_2\begin{pmatrix}2\\1\\0\\0\\0\end{pmatrix}+x_5\begin{pmatrix}1\\0\\-2\\0\\1\end{pmatrix}$$Nebenbei haben wir auch noch eine Basis des 2-dimensionalen Kerns erhalten ;)

Comments

Ist die Lösungsmenge Sol(A,b) des Gleichungssystems Ax = b dann die leere Menge?

---

Kannst du mir biite bei dieser Frage helfen?

Bestimmen Sie die Lösungsmenge Sol(A,c) des Gleichingssystems Ax=c.

---

Sol(A,c) habe ich gescahfft aber ich weiß es nicht, wie das genau mit Sol(A,b) ist. :(

---

Dazu musst du in der Rechnung an Stelle der Nullspalte den Vektor $\vec b$ eintragen und dann das Gleichungssystem auf die gleiche Weise lösen, wie wir es hier zusammen getan haben.

Answer 2

Bestimmen Sie eine Basis von Ker A

Löse die Gleichung $A\cdot \vec{x} = \vec{0}$.

Comments

Und wie geht das genau? :")

---

Ich komme trozdem nicht weiter.

---

Bitte hilf mir!!! :(

---

Kann ich erste Zeile mit zweite Zeile tauschen?

---

Die Lösungsmenge eines Gleichungssystems hängt nicht von der Reihenfolge der Gleichungen ab. Du darfst deshalb die Gleichungen eines Gleichungssystems vertauschen.

---

Klar darfst du das !

---

Ich komme leider seit 3 Stunden nicht mehr weiter.

---

Wie weit bist du gekommen?

---

1 -2 1 -1 1    | -1 -2

1 -2 -1 1 -3   | 2  -2

-3 6 2 -3 7    | -4  6

1 -2 1 1 1     | -2  -2

6 -12 -1 0 -8 | 5 -12

-------------------------------

1 -2 1 -1 1    | -1  -2

0 0 -2 2 -4    | 3    0

0 0 5 -6 10   | -7  0

0 0 0  2  0    | -1  0

0 0 -7 6 -14  | 11 0

---------------------------------

Und wie geht das weiter?

---

Addiere zum doppelten der fünften Zeile das siebenfache der zweiten Zeile.

Addiere zum doppelten der dritten Zeile das fünfache der zweiten Zeile.