Es seien C,D ∈ ℝ. Nun soll ich zeigen, dass die Folge konvergiert:
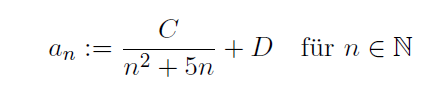
Text erkannt:
\( a_{n}:=\frac{C}{n^{2}+5 n}+D \quad \) für \( n \in \mathbb{N} \)
Um dies zu zeigen soll ich diese Definition verwenden:
Eine Folge (an)n∈ℕ reeller zahlen heißt konvergent mit Grenzwert a ∈ ℝ, falls gilt:
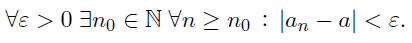
Text erkannt:
\( \forall \varepsilon>0 \exists n_{0} \in \mathbb{N} \forall n \geq n_{0}:\left|a_{n}-a\right|<\varepsilon \)
Notation:
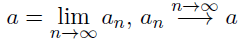
Ich weiß hier nicht genau wie ich anzufangen habe, kann mir da jemand helfen?
Danke!
Text erkannt:
\( a=\lim \limits_{n \rightarrow \infty} a_{n}, a_{n} \stackrel{n \rightarrow \infty}{\longrightarrow} a \)