Hallo,
wenn man ein Rechteck mit dem Seitenverhältnis von \(\sqrt 2\div 1\) an der schmaleren Seite halbiert ...
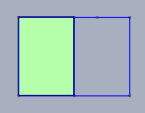
... bekommt man zwei neue Rechtecke mit dem identischen Seitenverhältnis.
Und wenn man von einem Rechteck mit dem Seitenverhältnis \(\Phi\div 1\) ein Quadrat abschneidet ....
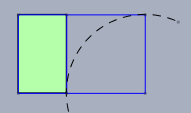
... bleibt ein Rechteck mit dem identischen Seitenverhältnis stehen.
beide Zahlen haben eine 1'er Periode in der Kettenbruchentwicklung:$$\begin{aligned} \Phi &= [1;\,\overline 1]\\\sqrt 2 &= [1;\,\overline 2]\end{aligned}$$und da die Zahl \(\Phi\) das mit einer \(1\) macht, gilt sie als irrationalste Zahl.
Bem.: Die nächste Zahl mit einer 1'er Periode, die ich gefunden habe, ist$$\frac{\sqrt{13}-1}{2} = [1;\,\overline 3]$$Gruß Werner