Liebe Forum-Mitglieder,
ich habe eine Frage zu folgender Nabla-Identiät:
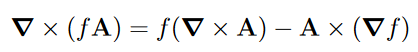
Links steht ein Kreuzprodukt dessen Ergebnis stets ein Vektor ist. Auf der rechten Seite dagegen haben wir Skalarfeld, von dem ein Kreuzprodukt abgezogen wird. Aber Ergebnis eines Skalarfeldes ist doch stets ein Skalar. Dann würden wir doch auf der rechten Seite der Gleichung einen Vektor von einem Skalar abziehen, oder?
Irgendwie ist mir die Notation mit dem Skalarfeld noch nicht ganz klar und würde mich auf jede Hilfe freuen!
EDIT:
Man nehme z.B. folgendes Beispiel: Wie kann das hinkommen? Auf der rechten Seite würde stets Skalar - Vektor stehen...
\( f(\mathbf{r})=x \quad \) und \( \quad \mathbf{A}(\mathbf{r})=\left(0, y \mathrm{e}^{z}, x\right)^{T}, \quad \) mit \( \quad \mathbf{r}=(x, y, z)^{T} \in \mathbb{R}^{3} \)
LG,
Hybridorbital