Bestimmen Sie Gleichungen für die zwei Geraden mit Steigung -\frac{1}{2} , die Tangenten an den Graph von …

Question

Aufgabe:

Bestimmen Sie Gleichungen für die zwei Geraden mit Steigung \( -\frac{1}{2} \), die Tangenten an den Graph von \( f(x)=\frac{2}{x-2}+2 \) sind.

Problem/Ansatz:

Ist meine Lösung so richtig?

f'(x)=-2/(x-2)^2
Geradengleichung der Tangente:
t=T(x)=a(x-x0)+b
a= f'(x0), b=f(x0)
y=T(x)= f(x0) +f'(x0)*(x-x0)
y=(2/(x-2))+(-2/(x-2)^2)*(x-x0)

Answer 1

Du hast in keiner Weise berücksichtigt, dass die erste Ableitung an den gesuchten Stellen den Wert \( -\frac{1}{2} \) annehmen muss.

Comments

Also es müssen noch die beiden Tangentenfunktionen berechnet werden bei denen die Steigung -1/2 ist.

Was mache ich danach?

---

Was mache ich danach?

Diese Frage darfst gern später stellen (wenn du die Punkte des Graphen ermittelt hast, in den der Tangentenanstieg den Wert -0,5 hat).

Answer 2

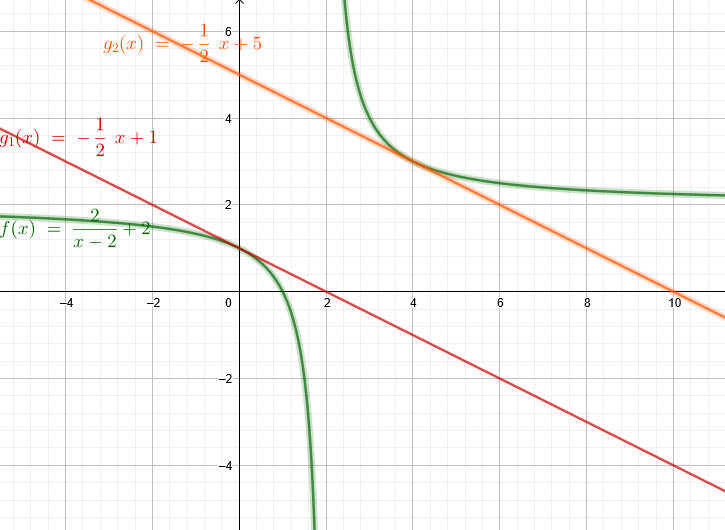
Alternativer Weg ohne Differenzieren:

\( f(x)=\frac{2}{x-2}+2 \)         \(g(x)=-\frac{1}{2}*x+b \)

\( f(x)=g(x)\)

 \( \frac{2}{x-2}+2=-\frac{1}{2}*x+b|*(x-2) \)

\( 2+2*(x-2)=-\frac{1}{2}*x^2-x+b*x-2b \)

\( 2*x-2=-\frac{1}{2}*x^2+x+b*x-2b|*2 \)

\( x^2+x*(2-2b)=4-4b \)

\( [x+(1-b)]^2=4-4b+(1-b)^2|\sqrt{~~} \)

\( x+(1-b)=+-\sqrt{4-4b+(1-b)^2} \)

\( +-\sqrt{4-4b+(1-b)^2}=0 \)

\(b₁=1\)

\(b₂=5\)

1.Tangente:

 \(g1(x)=-\frac{1}{2}*x+1 \)

2.Tangente:

\(g2(x)=-\frac{1}{2}*x+5 \)