Aufgabe:
ermittle zwei punkte des graphens der funktion f:R->R und zeichne den Graphen
Problem/Ansatz:
kann mir wer erklären wie diese aufgabe generell geht… lösungen wären auch nett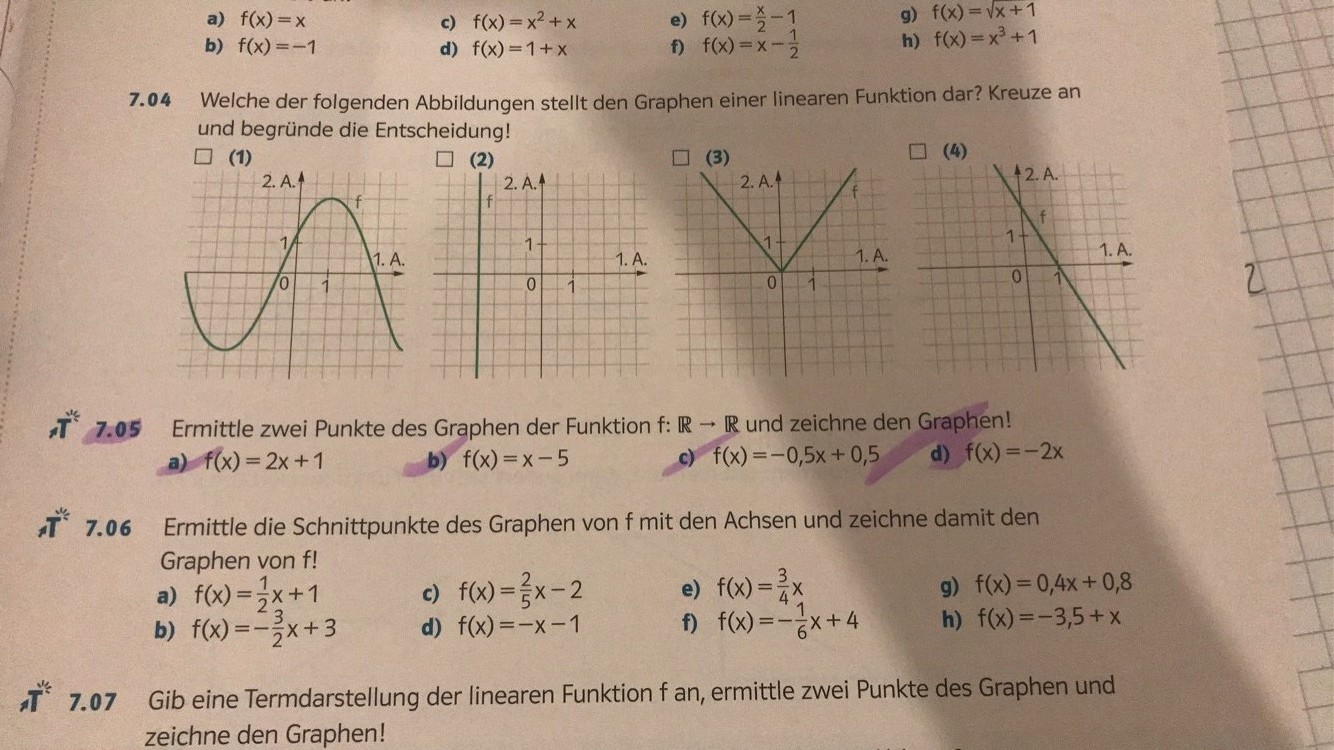
Text erkannt:
a) \( f(x)=x \)
c) \( f(x)=x^{2}+x \)
e) \( f(x)=\frac{x}{2}-1 \)
g) \( f(x)=\sqrt{x+1} \)
b) \( f(x)=-1 \)
d) \( f(x)=1+x \)
f) \( f(x)=x-\frac{1}{2} \)
h) \( f(x)=x^{3}+1 \)
7.04 Welche der folgenden Abbildungen stellt den Graphen einer linearen Funktion dar? Kreuze an und begründe die Entscheidung!
ง \( \mathbb{T}^{*} \) 7.05 Ermittle zwei Punkte des Graphen der Funktion \( \mathrm{f}: \mathbb{R} \rightarrow \mathbb{R} \) und zeichne den Graphen!
a) \( f(x)=2 x+1 \)
b) \( f(x)=x-5 \)
c) \( f(x)=-0,5 x+0,5 \)
d) \( f(x)=-2 x \)
A* \( 7.06 \) Ermittle die Schnittpunkte des Graphen von f mit den Achsen und zeichne damit den
Graphen von \( f \) !
a) \( f(x)=\frac{1}{2} x+1 \)
c) \( f(x)=\frac{2}{5} x-2 \)
e) \( f(x)=\frac{3}{4} x \)
g) \( f(x)=0,4 x+0,8 \)
b) \( f(x)=-\frac{3}{2} x+3 \)
d) \( f(x)=-x-1 \)
f) \( f(x)=-\frac{1}{6} x+4 \)
h) \( f(x)=-3,5+x \)
A \( 7.07 \) Gib eine Termdarstellung der linearen Funktion f an, ermittle zwei Punkte des Graphen und zeichne den Graphen!