Differenzierung und deren Definition

Question

Eine Funktion f: (a, b) → R heißt im Punkt x ϵ (a,b) differenzierbar, falls

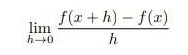
existiert, d.h. falls der Grenzwert 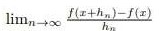für jede Folge (h_n) mit h_n → existiert und unabhängig von der Wahl der Folge ist. Falls f im Punkt x differenzierbar ist, schreibt man f '(x) für diesen Grenzwert. Eine Funktion, die in jedem Punkt ihres Definitionsbereiches differenzierbar ist, nennt man differenzierbar.

Zeigen Sie anhand dieser Definition, dass die Funktion f: R → R, f(x) = 2x³ - 1 differenzierbar ist mit f '(x) = 6x².

Wie stelle ich das an? Bitte um Rat

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Wir sollen zeigen, dass die der Patient \(f(x)=2x^3-1\) differenzierbar ist.

Zu diesem Zweck formen wir zunächst den Differenzenquotienten$$\phantom=\frac{f(x+h)-f(x)}{h}=\frac{(\;2(x+h)^3-1\;)-(2x^3-1)}{h}$$so um, dass das \(h\) aus dem Nenner verschwindet, damit wir den Grenzwert \(h\to0\) bilden können, ohne durch Null zu dividieren:$$=\frac{2(x+h)^3\pink{-1}-2x^3\pink{+1}}{h}=\frac{2(x^3+3x^2h+3xh^2+h^3)-2x^3}{h}$$$$=\frac{\pink{2x^3}+6x^2h+6xh^2+2h^3\pink{-2x^3}}{h}=\frac{6x^2h+6xh^2+2h^3}{h}$$$$=\frac{6x^2h}{h}+\frac{6xh^{2}}{h}+\frac{2h^3}{h}=6x^2+6xh+2h^2$$

Nun können wir den Grenzwert bequem angeben:$$f'(x)=\lim\limits_{h\to0}\frac{f(x+h)-f(x)}{h}=\lim\limits_{h\to0}\left(6x^2+6xh+2h^2\right)=6x^2+6x\cdot0+2\cdot0^2=6x^2$$

Comments

Ahhh okay jetzt ist mir alles klar geworden

---

Ich bedanke mich vielmals für ihre ausführliche Hilfe werter Herr.

Answer 2

f '(x) = 6x^2
Was ist der Defintionsbereich der Funktion ?
D = - ∞ .. + ∞
Es gibt keine Einschränkungen z.B Polstellen oder
Sprungstellen.

Comments

Entschuldigung aber das war leider nicht die Frage.