"Gegeben sind im Koordinatensystem (Einheit 1 cm) Die Punkte A (-2 / -1) und B (4 / 5)"
a) Berechne die Länge der Strecke AB
Der Satz des Pythagoras ist Dir bekannt? Dann kannst Du ihn anwenden mit der einen Kathete (4 - (-2)) und der anderen Kathete (5 - (-1)), also sind die Katheten jeweils 6 cm lang.
Länge2 = (6cm)2 + (6cm)2
Länge = √(72cm)2 ≈ 8,49cm
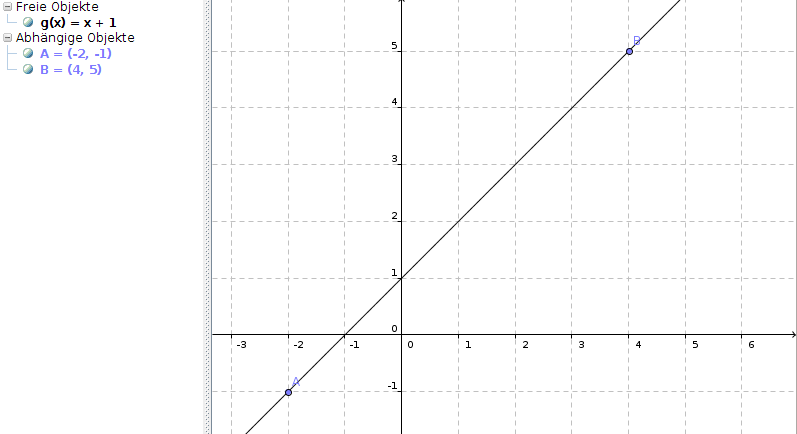
b) Verlängere die Strecke AB über A und B hinaus; du erhältst eine Gerade g. Bestimme die Gleichung g.
Geradengleichung allgemein
y = mx + b
m ist die Steigung, die man erhält, indem man die "y-Differenz" durch die "x-Differenz" dividiert:
m = (5 - (-1))/(4 - (-2)) = 6 / 6 = 1
b ist der y-Achsenabschnitt, den wir erhalten, indem wir einen Punkt, zum Beispiel B (4|5) in die bis jetzt berechnete Geradengleichung einsetzen:
y = 1 * x + b
5 = 1 * 4 + b
b = 1
Damit lautet die Geradengleichung
g(x) = x + 1
Besten Gruß