Bestimme die Gleichung der Geraden

Question

Aufgabe: Bestimme die Gleichung der Geraden durch den Punkt (8|-8) und Schnittpunkt mit der x-Achse bei 2.

Problem/Ansatz:

y=m*x+b

-8=m*8+b

0=m*2+b

Jetzt würde ich Additionsverfahren anwenden, um b zu eliminieren

-8=6*m

m=-8/6=-4/3

Dieses m einsetzen

-8=-4/3*8+b

b=-8+4/3*8

Stimmt das?

Comments

Stimmt das?

Du könntest mit den berechneten Daten mal die Funktion aufstellen und damit die Probe machen. Dann würdest du sehen das deine Lösung richtig ist.

Zumindest bisher. Aber ich glaube schon, dass dein Taschenrechner die Rechnung nach Eingabe auch ausrechnen kann.

Answer 1

f(x) =y = mx+b

f(8)= -8

f(2)= 0

8m+b= -8

2m+b= 0

subtrahieren:

6m= -8

m= -8/6 = -4/3

einsetzen:

2*(-4/3) +b= 0

b= 8/3

y= -4/3*x+8/3

Bestimme die Gleichung der Geraden durch den Punkt (8|-8) und Schnittpunkt mit der x-Achse bei 2.

Answer 2

Bestimme die Gleichung der Geraden durch den Punkt (8 | -8) und Schnittpunkt mit der x-Achse bei 2. (2 | 0)

Steigung

m = (- 8 - 0) / (8 - 2) = - 8/6 = - 4/3

Funktion in Punkt-Steigungs-Form

f(x) = - 4/3 * (x - 2) + 0
f(x) = - 4/3 * x + 8/3

Answer 3

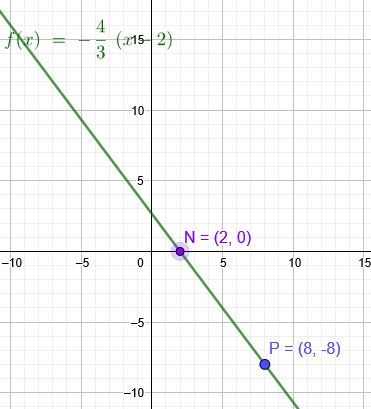
Aufgabe: Bestimme die Gleichung der Geraden durch den Punkt \(P(8|-8)\) und Schnittpunkt mit der x-Achse bei \(2\).

Lösung mit der Nullstellenform der Geraden:

Allgemein: \(f(x)=a*(x-N)\)

Schnittpunkt mit der x-Achse bei \(2\):

\(f(x)=a*(x-2)\)

\(P(8|-8)\):

\(f(8)=a*(8-2)\)

\(6a=-8\)     →\(a=-\frac{4}{3}\)

\(f(x)=-\frac{4}{3}*(x-2)\)