Gegeben sind Funktionen f1 (x) = -0,6 x² -5x - 6,4 ; D(f1) = IR und f2(x) = 14/15 x² +5 11/15 x +2 4/5 D(f2) = IR
f1(x) = - 0.6·x^2 - 5·x - 6.4
f2(x) = 14/15·x^2 + 86/15·x + 14/5
a) Bestimmen Sie die Schnittpunkte S1 und S2 der Graphen der beiden Funktionen!
f1(x) = f2(x)
-0.6·x^2 - 5·x - 6.4 = 14/15·x^2 + 86/15·x + 14/5
-0.6·x^2 - 5·x - 6.4 - (14/15·x^2 + 86/15·x + 14/5) = 0
-23/15·x^2 - 161/15·x - 46/5 = 0
Lösung mit abc-Formel
x1 = -1 und x2 = -6
f1(-1) = -2
f1(-6) = 2
P1(-1 | -2) P2(-6 | 2)
b) Bestimmen Sie den Funktionsterm der linearen Funktion, deren Graph S1 und S2 verbindet!
g(x) = (y1-y2)/(x1-x2) * (x - x1) + y1 = (-2 - 2) / (-1 - (-6)) * (x - (-1)) + (-2) = - 4/5·x - 14/5
c) Bestimmen Sie die Achsenschnittpunkte der Graphen aller drei Funktionen!
f1(0) = -6,4
f2(0) = 2,8
g(x) = -2,8
f1(x) = 0
-0.6·x^2 - 5·x - 6.4 = 0
x1 = -1.579304217 ∨ x2 = -6.754029116
f2(x) = 0
14/15·x^2 + 86/15·x + 14/5 = 0
x = -0.5349598707 ∨ x = -5.607897272
g(x) = 0
x = x = -3,5
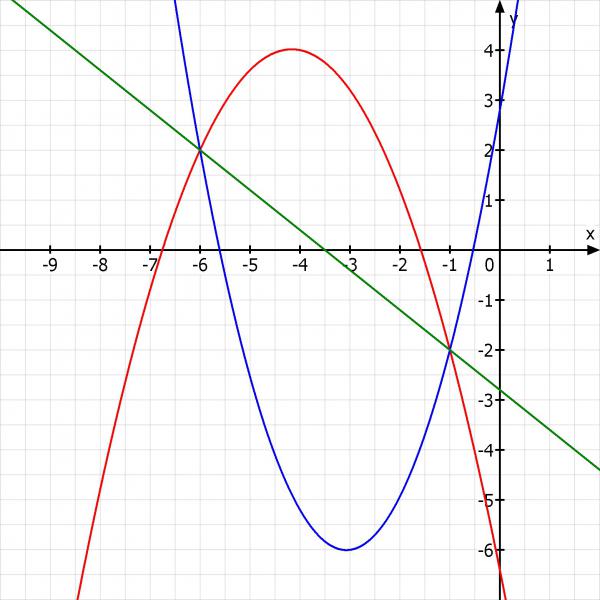
Hier noch die Skizzen: