Finden einer Formel zur Berechnung der Bogenlänge zwischen zwei Kreisen des selben Durchmesser mit konstanter Rautiefe
Hallo alle zusammen,
Ich hab hier ein Problem aus der Praxis ich Versuche eine Formel für das Fräsen von Konturen, mit gleich bleibender Rautiefe (Rz) an der Kontur zu finden
Es gibt die Formel zum berechnen von konstantem vf an der wkz Schneide
Innenkreis:
F_Kreis = ( ( R_Teil - R_Wkz ) / R_Teil) * F_Gerade
Außenkreis:
F_Kreis = ( ( R_Teil + R_Wkz ) / R_Teil) * F_Gerade
Nun möchte ich eine Formel aufstellen zum berechnen von konstanter Rz an der wkz Schneide
Ich hab das alles mal auf gezeichnet um es besser zu erklären Ich habe einen Fräser Ø8 der fährt mit einem fz von 2mm
Malen wir das mal auf, messen die Rauhigkeit/Abweichung und bekommen so einen Wert von 0,127:
Bild 1
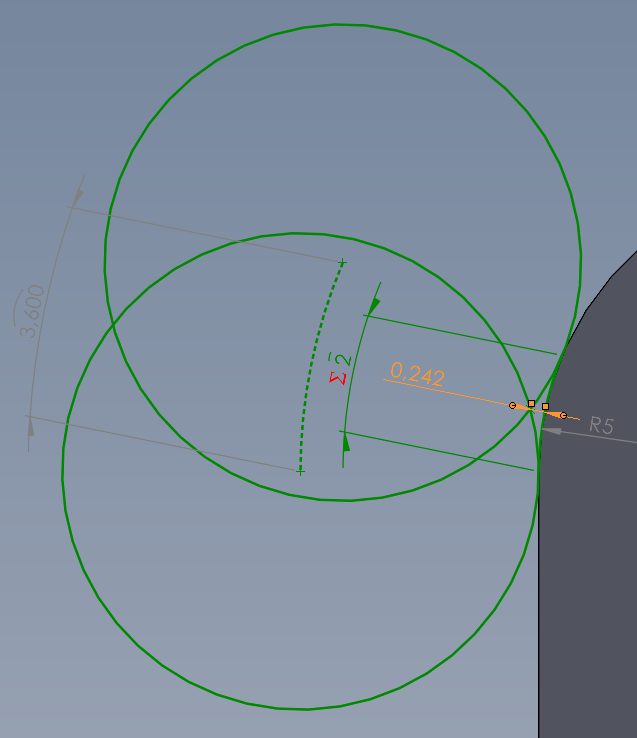
Wenn wir den Vorschub auf eine Aussenecke mit R5 umrechnen kommen wir auf fz 3,6.
Malen wir das mal auf, messen die Rauhigkeit/Abweichung und bekommen so einen Wert von 0,242:
Bild2
Und das ist zu viel, ich will nur eine Rauhigkeit/Abweichung wie auf der Geraden!
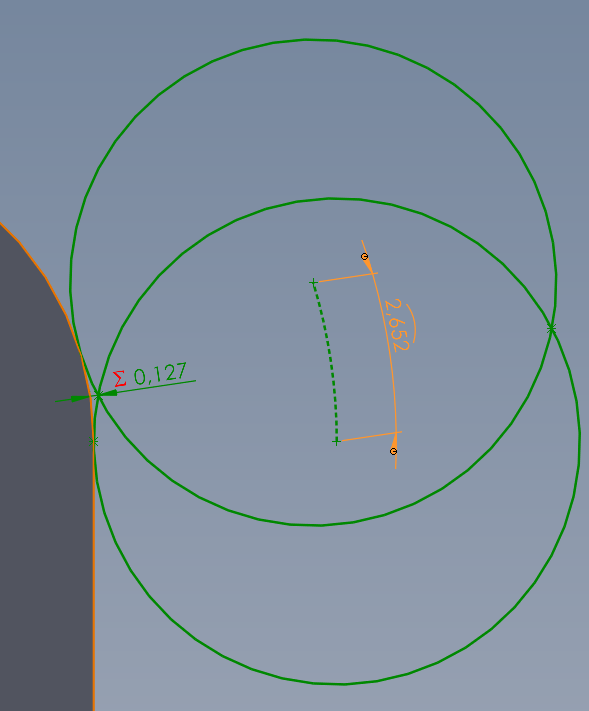
Malen wir das mal auf und messen den fz umd kommen auf 2,652
Bild3
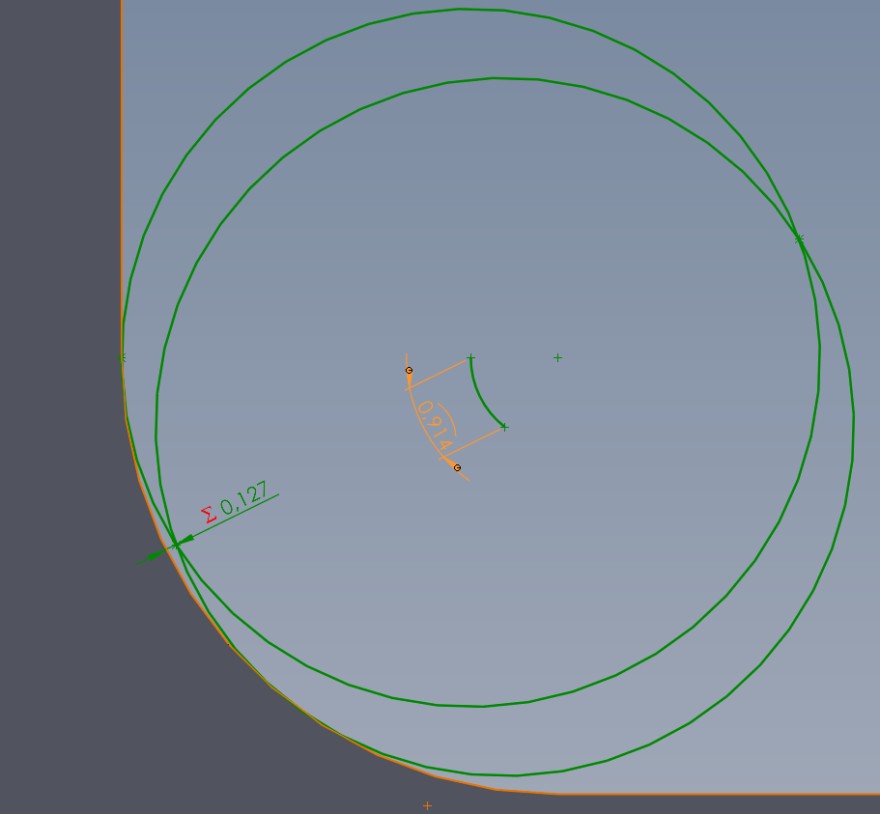
In der Innenecke ist das anders herum, der nach der Formel umgerechnete fz ist 0,4 wir können aber 0,914 fahren bei gleicher Abweichung.
Bild 4
Jetzt möchte ich eine Formel aufstellen so einfach wie möglich
Gegeben
Rz= Fix wert bsb. (0.1)
Ø-Fräser = Fix wert bsb. (8)
Fz = variabel (das soll errechnet werden )
Und dann haben wir noch
R Aussen
R Innen
Zuerst müssen Wir die Rauhtiefe Berechnen
Rz= D/2 - (√ (d²-Fz²)/4)
Anschließend müssen Wir von Rz nach Fz Bei Innen,Ausen Radien Umrechnen.
Aber mir fällt keine einfache Lösung ein
Vielleicht hat jemand einen Denkanstoß ich bin über jede Hilfe dankbar
Mit freundlichen Grüßen
Benjamin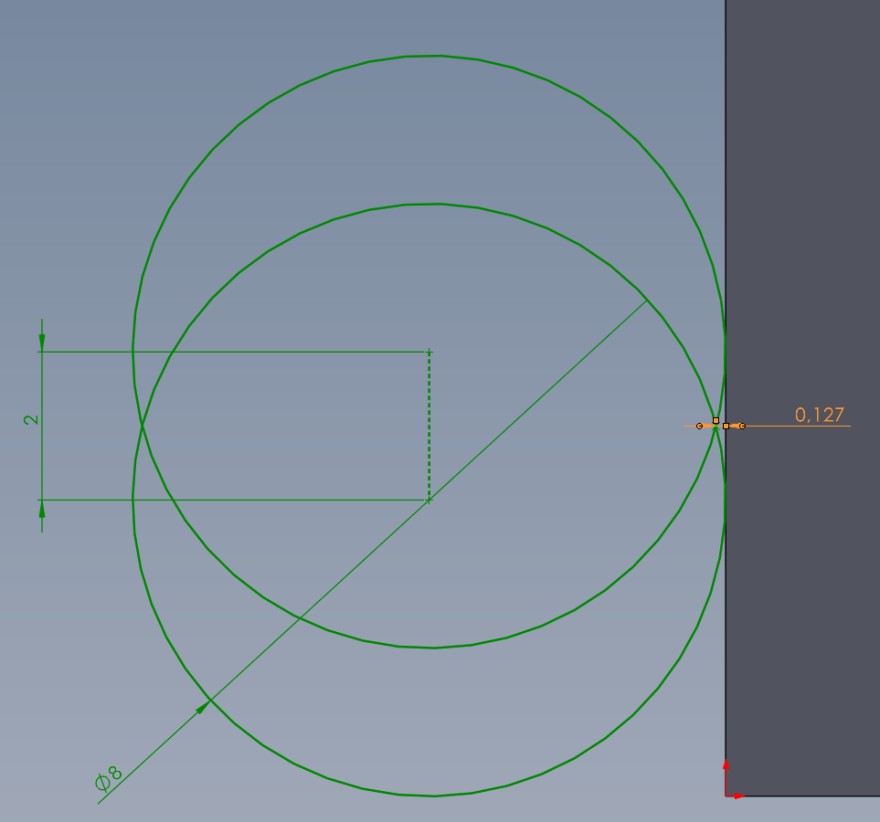
 Jo
Jo