Hallo
Ich denke ich weiß, wie man die Aufgabe löst.
Ich nehme an, dass H und R des Kegels konstant sind.
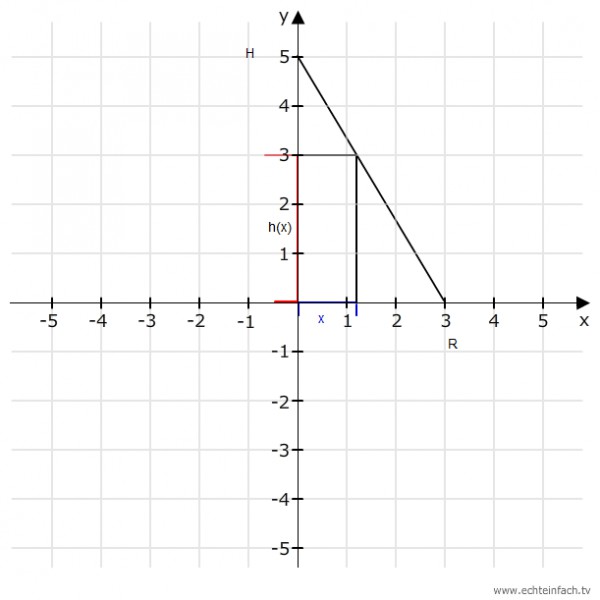
Zunächst einmal vereinfacht man das räumliche Problem auf ein ebenes Problem (s. Skizze). Man betrachet den Kegel von der Seite und kann dann die Höhe des Zylinders mit einer Geradengleichung beschreiben:
h(x) = H - x * (H/R)
Für den Radius des Zylinders gilt:
0 ≤ x ≤ R
Die Mantelfläche des Zylinders kann man mit:
MZ(x) = 2*π*x*h(x) beschreiben.
Um die Aufgabe zu lösen leitet man nun noch MZ(x) nach x ab und setzt es 0:
M'Z(x) = 0
M'Z(x) = 2*π * (H - x * (H/R) ) - 2*π*H/R * x
2*π * (H - x * (H/R) ) - 2*π*H/R * x = 0
x = R/2
Wenn also der Radius des Zylinders bei x = R/2 des großen Zylinders liegt, ist die Mantelfläche Maximal bezogen auf einen gegebenen Kegel.