In der Vorlesung wurde die Unabhängigkeit zweier Zufallsvariablen anhand eines Glücksradbeispiels erläutert (siehe Skript, Beispiel 1.38).
Beispiel 1.38
In den beiden folgenden Beispielen wird jeweils ein Glücksrad mit vier Ergebnismöglichkeiten einmal gedreht. Die Zufallsvariable \( X \) gibt die gedrehte Zahl im äußeren Ring und die Zufallsvariable \( Y \) die gedrehte Zahl im inneren Ring an.
(a) Glücksrad 1:
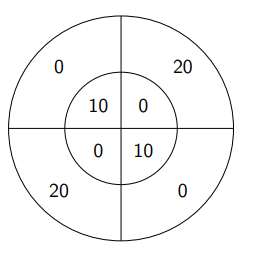
Dann haben wir die Wertebereiche \( W(X)=\{0,20\} \) und \( W(Y)= \) \( \{0,10\} \) sowie die folgende Verteilung:
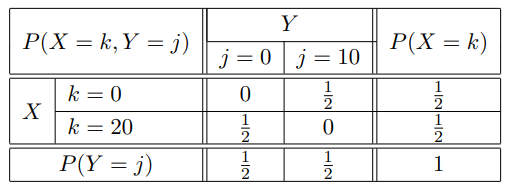
(b) Glücksrad 2:
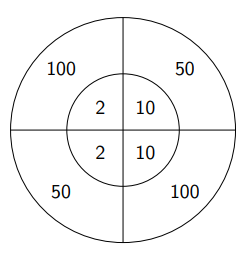
Dann haben wir die Wertebereiche \( W(X)=\{50,100\} \) und \( W(Y)=\{2,10\} \) sowie die folgende Verteilung:
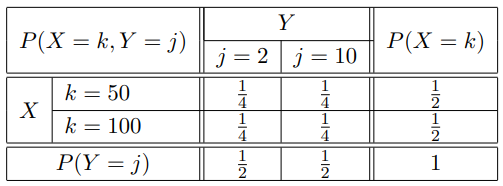
Wie wir am Beispiel der beiden Glücksräder gesehen haben, lassen sich aus der gemeinsamen Verteilung immer die Randverteilungen ableiten. Anders herum funktioniert dies nur in ganz bestimmten Fällen.
Stochastik II Stand 08.05.2015-2.pdf (0,7 MB) ( Vorlesung )
Aufgabe:
Geben Sie entsprechend dieses Beispiels zwei Glücksräder mit jeweils acht Feldern an. Eines so, dass die beiden Zufallsvariablen unabhängig sind, und eines so, dass sie nicht unabhängig sind.
Statt mit innerem und äußerem Zahlenkreis können Sie auch mit Farben und Zahlen o.ä. arbeiten.
Arbeiten Sie die Beispiele so aus, dass die Unabhängigkeit nachgewiesen bzw. widerlegt ist.