Zwei bijektive Abbildungen, und folgende Aussagen muss man beweisen:

Question

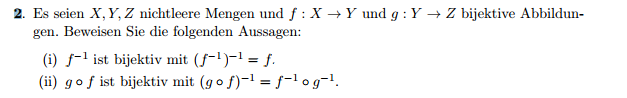
dass ist meine Aufgabe, die ich bekommen habe und bei i) komme ich nicht weiter.

Bei ii) habe ich darauf gefolgert, dass f^1 ο g^1 die Umkehrabbildung von g o f ist. Dazu habe ich einen kleinen Beweis angelegt, dass zu zeigen ist, dann ( f^1 ο g^1 ) (g o f) (x), für alle x∈X gilt.

Aber i) ist mir irgenwie zu Trivial, als das mir ein guter Beweis einfällt.

Ich hoffe auf eure hilfe.

Comments

so in etwa? 
Wenn f ^-1 bijektiv sein soll:

f ^-1 nicht injektiv, existiert kein f ^-1 

f ^-1 nicht surjektiv ist, muss der Bildbereich eingeschränkt sein

Wenn f ^-1 injektiv und nicht surjektiv für f : X → Y , X,Y ⊆ ℝ sein soll, dann ist (f ^-1)^-1 nicht injektiv , und es existiert gar kein (f ^-1)^-1

---

wenn nun f ^-1  bijektiv ist, ist auch (f ^-1 )^-1 bijektiv. So dass für jedes  y ∈ Y   es  genau ein  x ∈ X gibt mit f ^-1 (y) = x

und  für jedes x ∈ X   es  genau ein  y ∈ Y gibt mit (f ^-1 )^-1(x) = y = f(x)

---

sorry edit: wenn f ^-1 nicht surjektiv ist, muss der Bildbereich eingeschränkt werden bis f ^-1 surjektiv ist

---

mit f ^-1 : Bild(f) → X

---

vielleicht sollte man bei ii noch sagen, wenn g o f bijektiv ist, existiert eine Umkehrabbildung mit (g o f) ^{- 1}(z)  = f ^-1 o g ^-1 (z) so dass (g o f) ^{- 1}(z) nicht g ^-1 o f ^-1 sein kann da g o f eine Funktion g o f : X →Z  ist und die Umkehr eine Funktion (g o f) ^{- 1} : Z →X  ist

Answer 1

f^-1 bijektiv wäre vielleicht so zu zeigen:

1. Injektiv:   

Seien also a , b aus dem Definitionsbereich von f^-1 das ist  Y, weil

f surjektiv ist.    Und sei  f^-1(a)  =  f^-1 (b) .

Dann gibt es (wieder wegen der Surj. von f )

 u und v aus  X   mit  a= f(u)  und  b=f(v)

und nach Def. der Umkehrabb. ist    

f^-1(a)  =u   und     f^-1 (b) = v

Damit heißt   f^-1(a)  =  f^-1 (b) .

doch  u = v  und wegen a= f(u)  und  b=f(v)

und der Eindeutigkeit von f hast du  a=b .

Also ist f^-1 Injektiv.

Zur Surjektivität von f^-1 muss du zeigen:

Zu jedem x aus X gibt es ein y aus Y mit f^-1 (y) = x

Sei also  x aus X.  Da f auf ganz X definiert ist, gibt

es ein y aus Y mit  f(x) = y   also f^-1(y)  = x  nach Def.
der Umkehrabb.