Question

Bestimmen Sie alle z ∈ C fur die gilt: z^2 = ¯z

Brauche mal eure Hilfe, weiß nicht wie ich vorgehen soll.

Answer 1

z          = x+iy

z(quer)=x-iy

-> (x+iy)^2 = x-iy

x^2 + i2xy -y^2 = x-iy

Vergleich Real und Imaginärteil:

x^2 -y^2 = x

und

2xy= -y

usw.

Answer 2

Du kannst das sowohl in Polarkoordinaten als auch in kartesischen Koordinaten rechnen.

D.h. z= a + ib oder z = r * e^{i phi} einsetzen  und dann rechnen.

Polarkoordinaten:

z = r * e^{i (phi + 2kπ)}

z^2 = r^2 * e^{ i (2phi + 4kπ)}

z^quer = r * e^{  i ( -phi + 2kπ)}

Vergleichen:

r^2 = r ==> r = 1 oder 0 .

Für r=0 gilt z = 0. Erste Lösung! 

Für r ≠ 0, d.h. r=1 zusätzlich

2phi + 4kπ = - phi + 2kπ

3 phi = - 2kπ

phi = -2kπ / 3    ,

k einsetzen.

k = 0, phi_1  = 0 , zweite Lösung z = 1

k= 1, phi_2 = - 120°, dritte Lösung z = e^{-2πi/3}

k = -1, phi_3 = 120° , vierte Lösung z = e^{2πi / 3} 

Weitere Lösungen fallen mit den bereits angegebenen Lösungen zusammen.

Kontrolle:

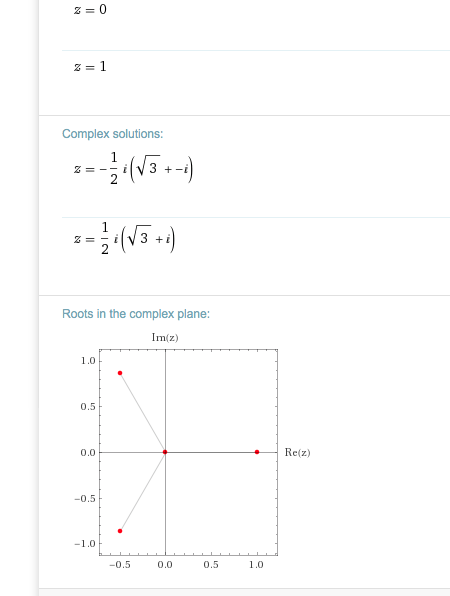
https://www.wolframalpha.com/input/?i=conjugate(z)+%3D+z%5E2