ich würde gerne dieses unbestimmte Integral berechnen
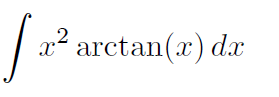
Meine Rechnung sieht bis jetzt so aus:
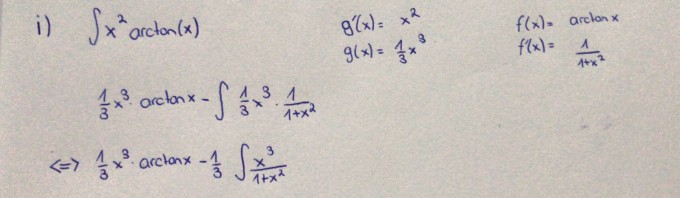
Die Frage ist nun wie kann ich x^3 / (1+x^2) integrieren?
In der Lösung steht folgendes:
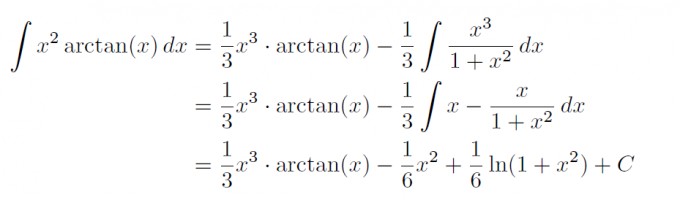
Aber wieso bzw. wie kommen die auf x- x/(1+x^2)? Gibt es eine Regel bzw. ein Hinweis den ich übersehen habe?
Würde mich sehr über Hilfe/Antworten freuen.