ich habe folgende Differentialgleichung:
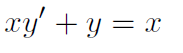
Umgestellt nach y':
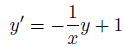
Also somit haben wir eine inhomogene Gleichung
f(x) = - 1 / x ; g(x) = 1
Lösung der Homogenen Gleichung:
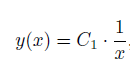
Nun Lösen wir die inhomogene Gleichung:
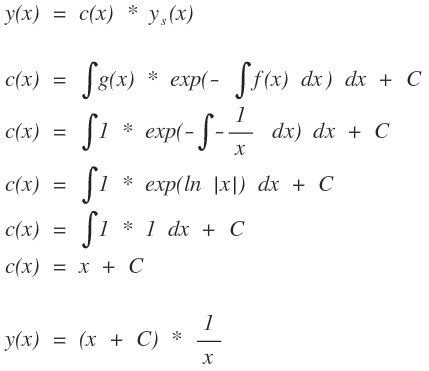
Hier muss irgendwo mein Fehler sein, die Lösung sagt nämlich folgendes:

Ich dachte e^{ln|x|} hebt sich auf und somit würde nur noch 1 da stehen und die 1 müsste ich nur noch integrieren zu x. Es wäre nett wenn mir jemand sagen könnten, wo mein Fehler genau liegt.
Euer Max :)