die Winkel im Punkt \(D\) sind der Schlüssel zur Lösung.
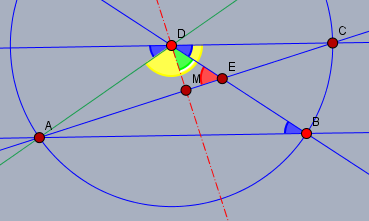
Die blauen Winkel sind alle gleich groß (\(34°\)). Daraus folgt dann der Winkel \(\angle ADC\) (gelb). Die rote Strich-Punkt-Gerade durch \(DM\) halbiert das Dreieck \(\triangle ACD\) und damit auch den Winkel \(\angle ADC\). Zieht man von der Hälfte den Winkel \(\angle BDC\) (blau) ab, so erhält man den Winkel \(\angle MDE\) (grün). Das Dreieck \(\triangle MED\) ist ein rechtwinkliges. $$\implies \epsilon = \angle DEA = 51°$$
"Mathematik ist ein wundersames Spiel mit überraschenden Zusammenhängen, eine Kunstform, die man ausfüllen kann wie Musik. Da steckt so viel Spannendes drin, das Mysterium der Primzahlen, die Magie der Endlos-Zahl Pi. Oder Geometrie, da kann ich weinen vor Begeisterung." Ranga Yogeshwar (aus Süddeutsche Zeitung vom 11.Juni 2019)