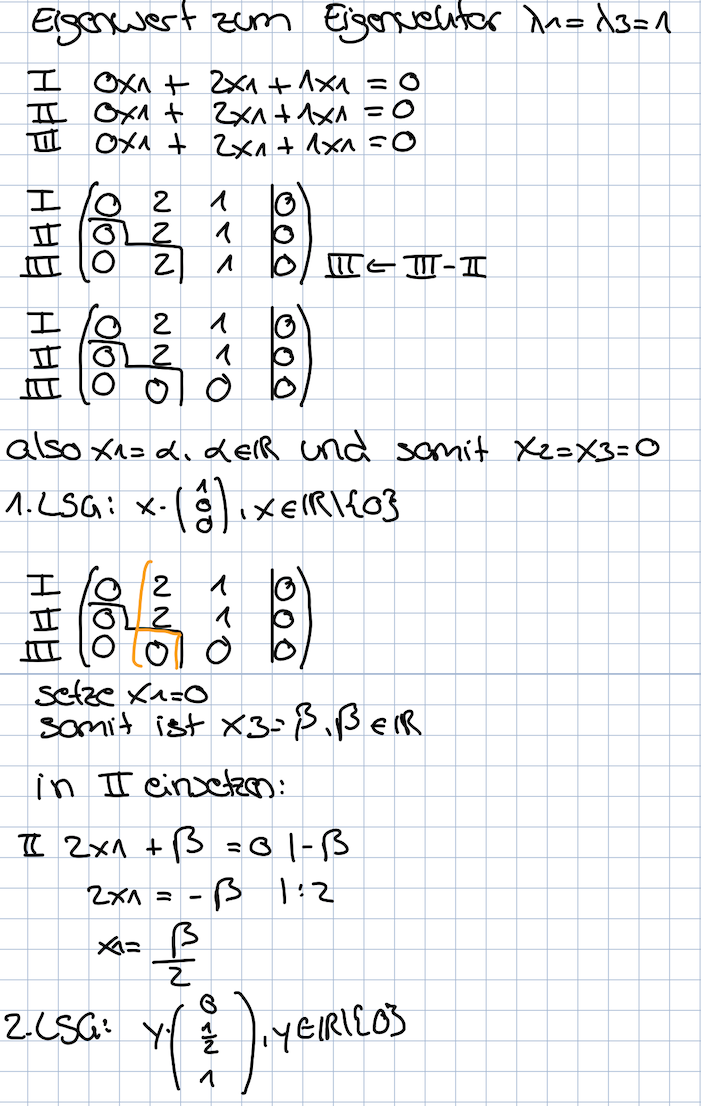Gegeben Sei folgende Matrix:
$$ B = \begin{matrix} 1 & 2 &1 \\ 0 & 3 & 1 \\ 0 & 2 & 2 \end{matrix} $$ nun soll davon die Eigenwerte und Eigenvektoren bestimmt werden.
$$ p(λ)= -λ^3+6 λ^2-9 λ+4 = 0 \\ \text{Eigenwerte: } λ_{1}= 1 \ λ_{2}= 4 \ λ_{3}= 1 $$
Die Eigenwerte sind laut Lösung korrekt.
$$ \text{Für den Eigenwert: } λ_{2} \text{ ist der Eigenvektor } w* \begin{pmatrix} 1\\1\\1\end{pmatrix}, w \in \mathbb{R}\ \text{\ ohne 0. Das ebenfalls richtig ist.} $$
Nun mein Problem:
Ich erhalte für die beiden anderen Eigenvektoren was anderes raus, als in der Lösung steht (siehe Bild).
Laut Lösung sollen zwei Vektoren mit $$ \begin{pmatrix} 1\\0\\0 \end{pmatrix} \ und\ \begin{pmatrix} 0\\1\\-2 \end{pmatrix} $$ rauskommen. Welches ich aber nicht genau nachvollziehen kann.