Hallo,
Willkommen in der Mathelounge!
Ist der Radius des horizontalen Kreises durch den Ellipsenmittelpunkt zugleich die Länge der kurzen Halbachse der entstandenen Ellipse?
Offensichtlich nicht, wie aus der folgenden Skizze hervor geht.
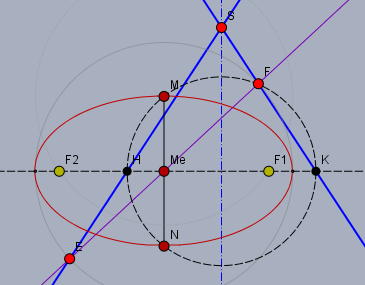
Oben siehst Du einen Kegel mit Spitze \(S\) längst seiner Achse (blaue Strich-Punkt-Linie) aufgeschnitten. Die dickeren blauen Geraden sind die Mantellinien. Die Schnittebene der Ellipse (rot) ist die lilane Gerade. Der Ellipsenmittelpunkt ist der Mittelpunkt \(M_e\) der Ellipsenachse \(EF\). Der horizontale Kreis, der \(M_e\) enthällt, ist schwarz gestrichelt eingezeichnet. Die kurze Halbachse der Ellipse ist \(M_eM\) bzw. \(M_eN\).
Die Länge der kurzen Halbachse ist immer kleiner als der Radius des horizontalen Kreises durch den Ellipsenmittelpunkt \(M_e\), weil im Falle eines Schrägschnitts \(M_e\) nicht mit dem Kreismittelpunkt zusammen fällt.
Falls etwas an der Zeichnung unklar ist, frage bitte nach.
Nachtrag:
Für den Fall, dass ein Kegel mit einem Öffnungswinkel von \(0°\) vorliegt, aber mit einem endlichen Durchmesser - also ein unendlich langer Zylinder(!), für diesen Fall ist die kurze Halbachse genauso lang wie der Kreisradius.
Ob man einen unendlich langen Zylinder dann als einen Kegel zulässt, sei dahin gestellt.
Gruß Werner