Aufgabe:
Einem spitzwinkligen Dreieck (Grundseite a, Höhe h) soll das flächengrösste Rechteck einbeschrieben werden, dessen eine Seite auf a liegt.
Problem/Ansatz:
1. Eine Skizze erstellt
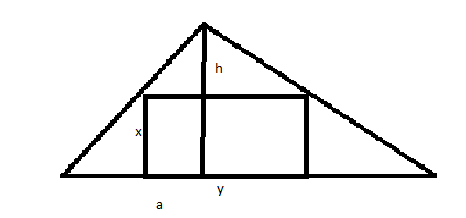
2. Erkenntnisse aufschreiben
Spitzwinkliges Dreieck = alle Winkel kleiner als 90°
3. Als nächstes stelle ich die Hauptbedingung auf
Arechteck = x*y
Wie komme ich auf die Nebenbedingung? Ich vermute irgend etwas mit dem Strahlensatz, komme jedoch nicht selber drauf.