Loglineare Regressionsgerade Rücktransformation

Question

Text erkannt:

\begin{tabular}{|l|l|l|l|l|l|}
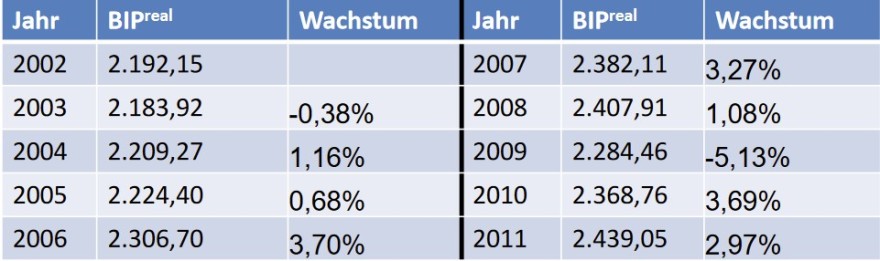
\hline Jahr & BIPreal & Wachstum & Jahr & BIPreal & Wachstum \\
\hline 2002 & $2.192,15$ & & 2007 & $2.382,11$ & $3,27 \%$ \\
\hline 2003 & $2.183,92$ & $-0,38 \%$ & 2008 & $2.407,91$ & $1,08 \%$ \\
\hline 2004 & $2.209,27$ & $1,16 \%$ & 2009 & $2.284,46$ & $-5,13 \%$ \\
\hline 2005 & $2.224,40$ & $0,68 \%$ & 2010 & $2.368,76$ & $3,69 \%$ \\
\hline 2006 & $2.306,70$ & $3,70 \%$ & 2011 & $2.439,05$ & $2,97 \%$ \\
\hline
\end{tabular}

Hi zusammen,

ich wollte gerade die logarithmisch lineare Regressionsgerade für diese Datenreihe berechnen nach der Formel ln(y)=a+b*ln(x).

Nun hab ich alle Werte logarithmiert, Kovarianz etc. berechnet und bin auf eine Regressionsgerade gekommen.

Die Regressionsgerade lautet: ln(y) = 7,611 + 0,085467 ln(x).

Nun wollte ich mal nachfragen, wie man diese loglineare Regressionsgerade rücktransformiert nach dem Schema y=a*x^b

Falls mir jemand helfen kann, bin ich sehr dankbar.

Vielen Dank im Voraus.

Liebe Grüße

Comments

Nachfragen bei

https://www.mathelounge.de/1032848/linear-logarithmische-regression

---

Und wie transformiert man die jetzt zurück?

Answer 1

ln (y) = a+b*ln(x)

(ln(y)--a)/b = ln(x)

x= e^((ln(y)--a)/b)) = e^(y/b - a/b)

Vertausche noch x und y.

Comments

Aber was setze ich denn dann am Ende für y ein?

Dann hätte ich ja e^(y/0,08546 -7,611/0,08546)

---

y= e^(x/b - a/b)

---

Vielen lieben Dank! extrem hilfreich!!