Bestimmen Sie die Matrix des Basiswechsels

Question

Aufgabe:

Basiswechsel
Betrachten Sie die Standardbasis \( \mathcal{A}=\left\{\boldsymbol{e}_{1}, \boldsymbol{e}_{2}\right\} \) und die Basis \( \mathcal{B}=\left\{\boldsymbol{e}_{1}^{\prime}, \boldsymbol{e}_{2}^{\prime}\right\}=\left\{2 \boldsymbol{e}_{1}+\boldsymbol{e}_{2}, 2 \boldsymbol{e}_{2}-\boldsymbol{e}_{1}\right\} \) von \( \mathbb{R}^{2} \). Außerdem sei \( F \) die orthogonale Projektion auf die durch den Vektor \( \mathbf{u}=\left(2 \boldsymbol{e}_{1}+\boldsymbol{e}_{2}\right) \) definierte Gerade.
b) Bestimmen Sie die Matrix des Basiswechsels von \( \mathcal{A} \) nach \( \mathcal{B} \) und umgekehrt; und multiplizieren Sie sie miteinander.
Hinweis: Schreiben Sie zunächst die Basisvektoren der Standardbasis bzgl. der neuen Basis \( \mathcal{B} \) auf.
c) Skizzieren Sie einen beliebigen Vektor \( \boldsymbol{x} \) und seine orthogonale Projektion \( F(\boldsymbol{x}) \). Zeigen Sie, dass die zu der linearen Abbildung \( F \) gehörigen Matrix in der Basis \( \mathcal{A} \) gegeben ist durch:
\( { }_{\mathcal{A}} F_{\mathcal{A}}=\frac{1}{5}\left(\begin{array}{ll} 4 & 2 \\ 2 & 1 \end{array}\right) \)

Hinweis: Die orthogonale Projektion \( F(\boldsymbol{x}) \) eines Vektors \( \boldsymbol{x} \) auf \( \boldsymbol{u} \) ist definiert durch:
\( F(\boldsymbol{x})=(\boldsymbol{x} \cdot \hat{\boldsymbol{u}}) \hat{\boldsymbol{u}} \)
wobei \( \hat{\boldsymbol{u}}=\boldsymbol{u} /|\boldsymbol{u}| \). Ist die Matrix \( { }_{\mathcal{A}} F_{\mathcal{A}} \) invertierbar?
d) Bestimmen Sie die zu der linearen Abbildung \( F \) gehörigen Matrix in der Basis \( \mathcal{B} \).

Problem/Ansatz:

Hallo zusammen,

dieses Thema bereitet mir nur Kopfschmerzen. Ich verstehe zwar, was ein Basiswechsel ungefähr ist, kann aber mit dieser Aufgabe überhaupt nichts anfangen.

Kann mich jemand vielleicht anleiten oder mir ein paar Hinweise dazu geben, was hier gefragt ist?

Vielen Dank und LG :-)

Comments

Habe die b) hinbekommen. Bräuchte aber noch einen Anstoß zur c)

Answer 1

Kann es sein, das da ein Druck/Abschreibfehler dabei ist?

\(\small \;_A{id}_{B} \, :=  \, \left(\begin{array}{rr}2&-1\\1&2\\\end{array}\right)\)

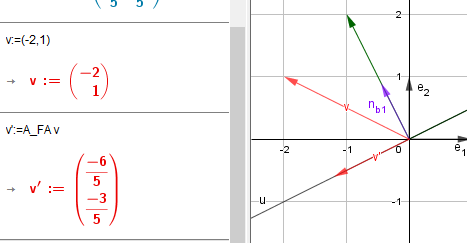
u=b₁ ⊥ n_b1 ={{0,-1},{1,0}} b₁/sqrt(b₁^2)

\(n_{b1} \, :=  \, \left( \begin{array}{r}\frac{-1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{array} \right)\)

die Projektion/Spiegelachse

u: n_b1 (x, y) = 0 ==> n_b1 (x, y) der Abstand von (x,y) von u

also die Projektion von (x,y) auf u

(x,y) - (n_b1 (x, y)) n_b1   |fehlt bei dir|

_AF_A = (id₂ - n_b1 n_b1^T)  || (x,y) ausklammern

\(_AF_A=\left(\begin{array}{rr}1&0\\0&1\\\end{array}\right) - \left( \begin{array}{r}\frac{-1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{array} \right) \left( \begin{array}{r}\frac{-1}{\sqrt{5}} &\frac{2}{\sqrt{5}} \end{array} \right) =  \left(\begin{array}{rr}\frac{4}{5}&\frac{2}{5}\\\frac{2}{5}&\frac{1}{5}\\\end{array}\right)\)

\(\,_BF_B = \;_A{id}_{B}^{-1} \,_AF_A \;_A{id}_{B}\)

- muss man gar nicht berechnen, wenn man genau hin schaut!