Aufgabe:
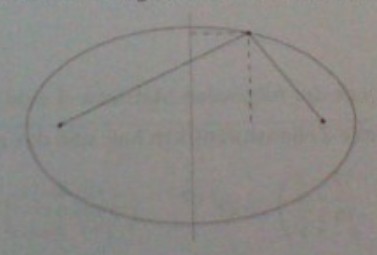
Es seien \( F_{1} \) und \( F_{2} \) verschiedene Punkte in der euklidischen Ebene mit Abstand \( 2 f \). Die Menge \( E \) der Punkte \( P \) der Ebene, für die die Summe der Abstände von \( P \) zu \( F_{1} \) und \( F_{2} \) einen konstanten Wert \( 2 a>2 f \) hat, ist definitionsgemāls eine Ellipse. Die Punkte \( F_{1} \) und \( F_{2} \) heißen die Brennpunkte der Ellipse.
Um zu einer Beschreibung der Ellipse in Koordinaten zu kommen, gehen wir so vor: Wir wählen ein kartesisches Koordinatensystem so, dass \( F_{1}=(-f, 0) \) und \( F_{2}=(f, 0) \).
Zeigen Sie:
\( E=\left\{(x, y) \in \mathbb{R}^{2} \mid\left(\frac{x}{a}\right)^{2}+\left(\frac{y}{b}\right)^{2}=1\right\} \)
wobei \( b=\sqrt{a^{2}-f^{2}} \). Man nennt a den großen und \( b \) den kleinen Halbmesser der Ellipse.