Stereometrie: Würfel in Halbkugel einbeschreiben. Kantenlänge?

Question

Frage: Berechnen Sie die Kantenlänge eines Würfels, der einer Halbkugel mit dem Radius a eingeschrieben werden kann.

Answer 1

Skizze:

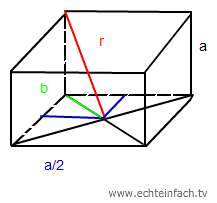
Die oberen vier Ecken des Würfels liegen jeweils auf der Kugelschale. Damit entspricht das r in der Skizze dem Radius der Halbkugel.

Zunächst berechnen wir b^2 = (a/2)^2 + (a/2)^2.

Dann r^2 = a^2 + b^2 = a^2 + (a/2)^2 + (a/2)^2.

a^2 ausklammern: r^2 = a^2 * (1 +1/4 +1/4) = 3/2 * a^2

Damit ist a = sqrt(2/3) * r  //nur positive Lösungen sind hier sinnvoll.

Comments

Leider falsch!