Hochpunkte und Tiefpunkte bei Sinus & Cosinus bestimmen

Question

habe hier eine Aufgabe aber ich weiß einfach nich wie ich die löen soll... a) f (x) = sin (x); x E [0;2pi  für Hilfe :)

Answer 1

An den Hochpunkten des Sinus gilt sin(x)=1, an den Tiefpunkten sin(x)=−1.
Benutze nun den Arcussinus, um die x-Koordinate zu bestimmen.

(Es gibt auch andere Möglichkeiten.)

Comments

Was is denn ein arcussinus ? Das kenn ich nicht :(

---

Arkussinus ist die Umkehrung des Sinus, man schreibt sin^-1() oder arcsin()

Beispiel:

sin(90°) = 1

sin^-1(1) = 90°

Siehe auch https://www.matheretter.de/wiki/sinus

---

Ist ja Alles schön und gut aber ich hab jetz noch ni h verstanden wie ich zu den hoch und tiefpunkten. Komme...:/

Answer 2

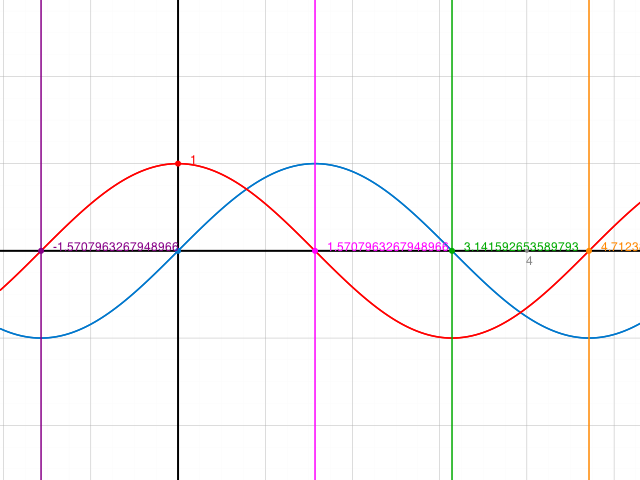
Rot ist hier Cosinus, blau Sinus. Jetzt ablesen

Die Hochpunkte des Cosinus liegen bei 0, 2pi, 4pi, -2pi...
Allgemein bei 2kpi, k Element Z

Die Tiefpunkte des Cosinus liegen bei pi, 3pi, 5pi, -pi...
Allgemein bei pi+ 2kpi, k Element Z

Die Hochpunkte des Sinus liegen bei pi/2, pi/2 + 2pi, pi/2 + 4pi, pi/2 - 2pi.
Allgemein bei pi/2 + 2kpi, k Element Z

Die Tiefpunkte des Sinus liegen bei 3pi/2, 3pi/2 + 2pi, 3pi/2 + 4pi, 3pi/2 - 2pi.
Allgemein bei 3pi/2 + 2kpi, k Element Z

Z: Menge der ganzen Zahlen.

Comments

Und Was is das mit dem Element ? Ich bin in der 10. Und ich bin mir jetz grad nich sicher ob ich das so machen muss der nicht doch einen andern weg nehmen muss...Mh..

---

Du brauchst nur die Lösungen in [0, 2pi] und kannst das Element Z vergessen.

Die Hochpunkte des Cosinus liegen bei 0 =0°, 2pi = 360°, falls da 2pi noch zum Intervall gehört.

Der Tiefpunkt des Cosinus liegen bei pi = 180°

Der Hochpunkt des Sinus liegen bei pi/2 = 90°

Der Tiefpunkt des Sinus liegt bei 3pi/2 = 270°

---

Ja das hab ich verstanden ok und Was heißt dieses komische E da bei x E [0;2pi] ?

---

Hi, x ∈ [0;2pi] bedeutet, dass x aus dem Intervall von 0 bis 2pi sein soll.
Es ist das Symbol für "ist Element aus" oder nur "Element aus".

---

Die schliessende Klammer fehlt halt in der Frage…

---

"Und was ist das mit dem Element? Ich bin in der 10. Und ich bin mir jetzt grad nicht sicher, ob ich das so machen muss oder nicht doch einen andern Weg nehmen muss... Mh..."

Die Extrempunkte von Sinus und Kosinus lassen sich auf ganz unterschiedliche Weise herleiten. Wenn Du eine zum Stoffzusammenhang passende Antwort erhalten möchtest, kann es nützen, wenn Du zu Deiner Frage auch den Stoffzusammenhang (also z.B. Jahrgangsstufe, Schulart, Kapitelüberschrift aus dem Lehrbuch usw.) in dem sich die Frage gestellt hat, mitteilst.